题目内容
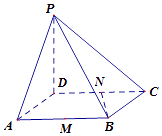
【题目】如图1,已知长方形ABCD中,AB=2,AD=1,E为DC的中点.将△ADE沿AE折起,使得平面ADE⊥平面ABCE. 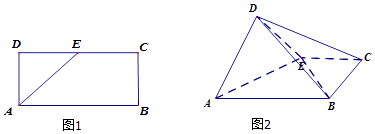
(1)求证:平面BDE⊥平面ADE
(2)求三棱锥 C﹣BDE的体积
【答案】
(1)证明:连接BE,∵长方形ABCD中,AB=2,AD=1,
E为DC的中点,DE=1,∴AE=BE= ![]()
∴AE2+BE2=2=AB2,∴BE⊥AE.
∵平面ADE⊥平面ABCE,平面ADE∩平面ABCE=AE,BE平面ABCE
∴BE⊥平面ADE,又∵BE平面BDE,
∴平面BDE⊥平面ADE.
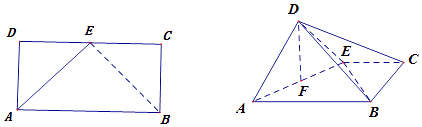
(2)解:取AE中点F,连结DF,
∵AD=DE,∴DF⊥AE,
又∵平面ADE⊥平面ABCE,且交线为AE,DF平面ADE,
∴DF⊥平面BCE
在Rt△ADE中,AD=DE=1,AE= ![]() ,∴DF=
,∴DF= ![]() ,
,
∴ ![]()
又∵VC﹣BED=VD﹣BCE,
∴三棱锥C﹣BDE的体积 ![]()
【解析】(1)连接BE,推民出BE⊥AE,从而BE⊥平面ADE,由此能证明平面BDE⊥平面ADE.(2)取AE中点F,连结DF,由VC﹣BED=VD﹣BCE,能求出三棱锥C﹣BDE的体积.
【考点精析】通过灵活运用平面与平面垂直的判定,掌握一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.

练习册系列答案
相关题目