题目内容
13.如图所示,算法流程图的输出结果为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{11}{12}$ | D. | $\frac{25}{24}$ |
分析 模拟执行程序框图,依次写出每次循环s,n的值,当n=8时,不满足条件m<8,退出循环,输出s的值为$\frac{11}{12}$.
解答 解:模拟执行程序框图,可得
s=0,n=2
满足条件m<8,s=$\frac{1}{2}$,n=4
满足条件m<8,s=$\frac{1}{2}$+$\frac{1}{4}$,n=6
满足条件m<8,s=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$=$\frac{11}{12}$,n=8
不满足条件m<8,退出循环,输出s的值为$\frac{11}{12}$.
故选:C.
点评 本题主要考查了循环结构的程序框图,依次写出每次循环s,n的值是解题的关键,属于基本知识的考查.

练习册系列答案
相关题目
3.已知f(x)=$\left\{\begin{array}{l}{cosπx(x≤0)}\\{f(x-1)+1(x>0)}\end{array}\right.$,则f($\frac{4}{3}$)+f(-$\frac{4}{3}$)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | 1 |
1.给出演绎推理的“二段论”,已知函数f(x)=$\frac{1}{x}$在(-∞,0)∪(0,+∞)是单调递减的,有因为-1<2,所以f(-1)>f(2),即-1$>\frac{1}{2}$,这显然是不对的,那么这个推理是( )
| A. | 大前提推理 | B. | 小前提推理 | C. | 推理形式错误 | D. | 非以上错误 |
2.将5名同学分到甲、乙、丙三个小组,若甲组至少两人,乙、丙两组每组至少一人,则不同的分配方案共有( )种.
| A. | 80种 | B. | 120种 | C. | 140种 | D. | 50种 |




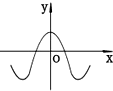
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,令${a_n}=f(\frac{nπ}{6})$,则a1+a2+a3+…+a2014=0.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,令${a_n}=f(\frac{nπ}{6})$,则a1+a2+a3+…+a2014=0.