题目内容
已知函数f(x)=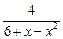 ,g(x)=x2-3ax+2a2(a<0),若不存在实数x使得f(x)>1和 g(x)<0同时成立,试求a的范围.
,g(x)=x2-3ax+2a2(a<0),若不存在实数x使得f(x)>1和 g(x)<0同时成立,试求a的范围.
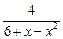 ,g(x)=x2-3ax+2a2(a<0),若不存在实数x使得f(x)>1和 g(x)<0同时成立,试求a的范围.
,g(x)=x2-3ax+2a2(a<0),若不存在实数x使得f(x)>1和 g(x)<0同时成立,试求a的范围.a的范围是{a|a≤-2或-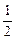 ≤a<0}.
≤a<0}.
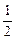 ≤a<0}.
≤a<0}.由f(x)>1,得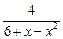 >1,
>1,
化简整理得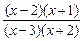 <0.
<0.
解得-2<x<-1或2<x<3.
即f(x)>1的解集为A={x|-2<x<-1或2<x<3}.
由g(x)<0得x2-3ax+2a2<0,
即(x-a)(x-2a)<0(a<0).
则g(x)<0的解集为B={x|2a<x<a,a<0}.
根据题意,有A∩B=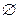 .
.
因此,a≤-2或-1≤2a<0.
故a的范围是{a|a≤-2或-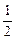 ≤a<0}.
≤a<0}.
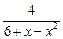 >1,
>1,化简整理得
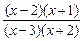 <0.
<0.解得-2<x<-1或2<x<3.
即f(x)>1的解集为A={x|-2<x<-1或2<x<3}.
由g(x)<0得x2-3ax+2a2<0,
即(x-a)(x-2a)<0(a<0).
则g(x)<0的解集为B={x|2a<x<a,a<0}.
根据题意,有A∩B=
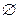 .
.因此,a≤-2或-1≤2a<0.
故a的范围是{a|a≤-2或-
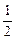 ≤a<0}.
≤a<0}.
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
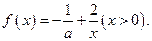 (1)解关于
(1)解关于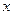 的不等式
的不等式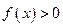 ;(2)若
;(2)若 在
在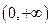 上恒成立,求实数
上恒成立,求实数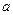 的取值范围。
的取值范围。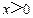 ,
,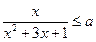 恒成立,则
恒成立,则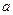 的取值范围是 .
的取值范围是 .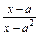 <0 (a∈R).
<0 (a∈R).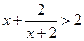 的解集是( )
的解集是( )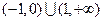

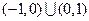

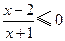 的解集是( )
的解集是( )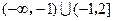
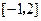
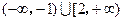
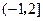
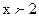 },则关于x的不等式
},则关于x的不等式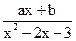 〉0的解集为( )
〉0的解集为( )