题目内容
(1)当a=
时,解不等式ax2+2x+1>0;
(2)当a∈R时,解关于x的不等式ax2+2x+1>0.
| 1 |
| 2 |
(2)当a∈R时,解关于x的不等式ax2+2x+1>0.
(1)当a=
时,不等式为x2+4x+2>0,
∴原不等式的解集为{x|x<-2-
或x>-2+
};
(2)当a=0时,原不等式的解集为{x|x>-
},
当a>0时,方程ax2+2x+1=0,△=4-4a,
①若△>0,即0<a<1时,方程ax2+2x+1=0的两个解为x1=
,x2=
,且x1<x2,
∴原不等式的解集为{x|x<
或x>
};
②若△=0,即a=1时,原不等式的解集为{x|x≠-1};
②若△<0,即a>1时,原不等式的解集为R;
当a<0时,一定有△>0,方程ax2+2x+1=0的两个解为x1=
,x2=
,且x1>x2,
∴原不等式的解集为{x|
<x<
}.
| 1 |
| 2 |
∴原不等式的解集为{x|x<-2-
| 2 |
| 2 |
(2)当a=0时,原不等式的解集为{x|x>-
| 1 |
| 2 |
当a>0时,方程ax2+2x+1=0,△=4-4a,
①若△>0,即0<a<1时,方程ax2+2x+1=0的两个解为x1=
-1-
| ||
| a |
-1+
| ||
| a |
∴原不等式的解集为{x|x<
-1-
| ||
| a |
-1+
| ||
| a |
②若△=0,即a=1时,原不等式的解集为{x|x≠-1};
②若△<0,即a>1时,原不等式的解集为R;
当a<0时,一定有△>0,方程ax2+2x+1=0的两个解为x1=
-1-
| ||
| a |
-1+
| ||
| a |
∴原不等式的解集为{x|
-1+
| ||
| a |
-1-
| ||
| a |

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
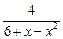 ,g(x)=x2-3ax+2a2(a<0),若不存在实数x使得f(x)>1和 g(x)<0同时成立,试求a的范围.
,g(x)=x2-3ax+2a2(a<0),若不存在实数x使得f(x)>1和 g(x)<0同时成立,试求a的范围.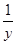 ,b=y+
,b=y+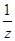 ,c=z+
,c=z+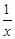 ,则a,b,c三数
,则a,b,c三数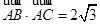 ,∠BAC=30°,设M是△ABC内的一点(不在边界上),定义f(M)=(x,y,z),其中
,∠BAC=30°,设M是△ABC内的一点(不在边界上),定义f(M)=(x,y,z),其中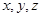 分别表示△MBC,△MCA,△MAB的面积,若
分别表示△MBC,△MCA,△MAB的面积,若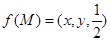 ,则
,则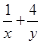 的最小值为__________________
的最小值为__________________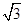
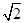
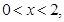 则函数
则函数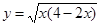 的最大值为
的最大值为