题目内容
(12分) 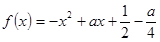 在区间[0,1]上的最大值为2,求
在区间[0,1]上的最大值为2,求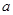 的值.
的值.
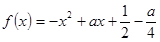 在区间[0,1]上的最大值为2,求
在区间[0,1]上的最大值为2,求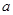 的值.
的值.f(x)在区间[0,1]上的最大值为2时a=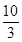 或-6.
或-6.
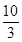 或-6.
或-6.本试题主要是考查了二次函数的在给定函数的区间上的最值。
需要对于函数对称轴与定义域的关系分类讨论得到结论。分为三种情况来得到。
解: f(x)=-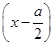 2+
2+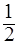 -
-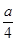 +
+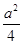 .
.
①当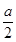 ∈[0,1],即0≤a≤2时,f(x)max=
∈[0,1],即0≤a≤2时,f(x)max=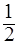 -
-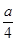 +
+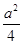 =2,
=2,
则a=3或a=-2,不合题意.
②当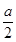 >1时,即a>2时,f(x)max=f(1)=2⇒a=
>1时,即a>2时,f(x)max=f(1)=2⇒a=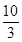 .
.
③当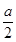 <0时,即a<0时,f(x)max=f(0)=2⇒a=-6.
<0时,即a<0时,f(x)max=f(0)=2⇒a=-6.
综上,f(x)在区间[0,1]上的最大值为2时a=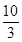 或-6.
或-6.
需要对于函数对称轴与定义域的关系分类讨论得到结论。分为三种情况来得到。
解: f(x)=-
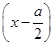 2+
2+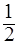 -
-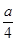 +
+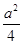 .
.①当
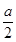 ∈[0,1],即0≤a≤2时,f(x)max=
∈[0,1],即0≤a≤2时,f(x)max=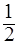 -
-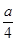 +
+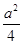 =2,
=2,则a=3或a=-2,不合题意.
②当
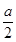 >1时,即a>2时,f(x)max=f(1)=2⇒a=
>1时,即a>2时,f(x)max=f(1)=2⇒a=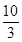 .
.③当
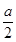 <0时,即a<0时,f(x)max=f(0)=2⇒a=-6.
<0时,即a<0时,f(x)max=f(0)=2⇒a=-6.综上,f(x)在区间[0,1]上的最大值为2时a=
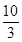 或-6.
或-6.
练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
 的顶点坐标为
的顶点坐标为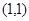 ,且
,且 ,
, ∈
∈ ,
, 的图象恒在
的图象恒在 的图象上方,
的图象上方, 的取值范围,
的取值范围, 上单调,求实数
上单调,求实数 的取值范围.
的取值范围. ,设函数
,设函数 ,
, ,且函数
,且函数 的值域为
的值域为 ,求
,求 在
在 上是单调函数,求实数
上是单调函数,求实数 的取值范围.
的取值范围. ,不等式
,不等式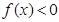 的解集是
的解集是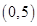 ,
, 的解析式;
的解析式; ,不等式
,不等式 恒成立,求t的取值范围.
恒成立,求t的取值范围. 在区间
在区间 上为增函数,则实数
上为增函数,则实数 的取值范围是( )
的取值范围是( )



 , 若
, 若 在区间
在区间 上的最大值为
上的最大值为 , 最小值为
, 最小值为 , 令
, 令 .
.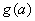 的函数表达式;
的函数表达式; x2-1的图像开口大小相同,开口方向也相同,y=f(x)的对称轴方程为x=1,图像过点(2,
x2-1的图像开口大小相同,开口方向也相同,y=f(x)的对称轴方程为x=1,图像过点(2,  )点
)点 是不共线的两向量,其夹角是
是不共线的两向量,其夹角是 ,若函数
,若函数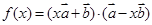 (
( )在
)在 上有最大值,则( )
上有最大值,则( ) ,且
,且 ,且
,且