题目内容
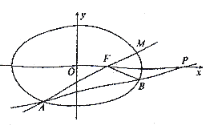
【题目】已知
为椭圆
上一点，
为椭圆长轴上一点，
为坐标原点，有下列结论：①存在点，，使得
为等边三角形；②不存在点，，使得为等边三角形；③存在点，，使得
；④不存在点，，使得.其中，所有正确结论的序号是( )
A.①④B.①③C.②④D.②③
【答案】A
【解析】
利用椭圆的简单几何性质，直接可判断①正确②错误，分情况讨论点
、
的位置，利用余弦定理判断
，即可确定③错误④正确.
过原点且倾斜角为
的直线一定与椭圆有交点，假设
轴右侧的交点
是，在长轴上取
，则
就是等边三角形
故①正确，②错误
若点和点在轴两侧，则一定是锐角
若点和点在轴同侧，不妨设为在轴右侧
设点
，则
，且
由椭圆性质可知，当点是长轴端点时，最大
因为
，
，
所以
所以
即
，故③错误，④正确
故选：A
练习册系列答案
相关题目
