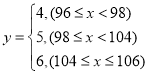题目内容
【题目】
对于各项均为整数的数列![]() ,如果
,如果![]() (
(![]() =1,2,3,…)为完全平方数,则称数
=1,2,3,…)为完全平方数,则称数
列![]() 具有“
具有“![]() 性质”.
性质”.
不论数列![]() 是否具有“
是否具有“![]() 性质”,如果存在与
性质”,如果存在与![]() 不是同一数列的
不是同一数列的![]() ,且
,且![]() 同
同
时满足下面两个条件:①![]() 是
是![]() 的一个排列;②数列
的一个排列;②数列![]() 具有“
具有“![]() 性质”,则称数列
性质”,则称数列![]() 具有“变换
具有“变换![]() 性质”.
性质”.
(I)设数列![]() 的前
的前![]() 项和
项和![]() ,证明数列
,证明数列![]() 具有“
具有“![]() 性质”;
性质”;
(II)试判断数列1,2,3,4,5和数列1,2,3,…,11是否具有“变换![]() 性质”,具有此性质的数列请写出相应的数列
性质”,具有此性质的数列请写出相应的数列![]() ,不具此性质的说明理由;
,不具此性质的说明理由;
(III)对于有限项数列![]() :1,2,3,…,
:1,2,3,…,![]() ,某人已经验证当
,某人已经验证当![]() 时,
时,
数列![]() 具有“变换
具有“变换![]() 性质”,试证明:当”
性质”,试证明:当”![]() 时,数列
时,数列![]() 也具有“变换
也具有“变换![]() 性质”.
性质”.
【答案】(I)证明见解析.(II)数列1,2,3,4,5具有“变换P性质”,数列![]() 为3,2,1,5,4.数列1,2,3,…,11不具有“变换P性质”理由见详解;(III)证明见解析.
为3,2,1,5,4.数列1,2,3,…,11不具有“变换P性质”理由见详解;(III)证明见解析.
【解析】
(I)当![]() 时,
时,![]()
![]() 又
又![]() .
.
所以![]() 是完全平方数,
是完全平方数,
数列![]() 具有“P性质”
具有“P性质”
(II)数列1,2,3,4,5具有“变换P性质”,
数列![]() 为3,2,1,5,4
为3,2,1,5,4
数列1,2,3,…,11不具有“变换P性质”
因为11,4都只有5的和才能构成完全平方数
所以数列1,2,3,…,11不具有“变换P性质”
(III)设![]()
注意到![]()
令![]()
由于![]() ,
,
所以![]()
又![]()
![]()
所以![]()
即![]()
因为当![]() 时,数列
时,数列![]() 具有“变换P性质”
具有“变换P性质”
所以1,2,…,4m+4-j-1可以排列成![]()
使得![]() 都是平方数
都是平方数
另外,![]() 可以按相反顺序排列,
可以按相反顺序排列,
即排列为![]()
使得![]()
![]()
所以1,2,![]() 可以排列成
可以排列成
![]()
满足![]() 都是平方数.
都是平方数.
即当![]() 时,数列A也具有“变换P性质”
时,数列A也具有“变换P性质”

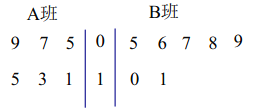
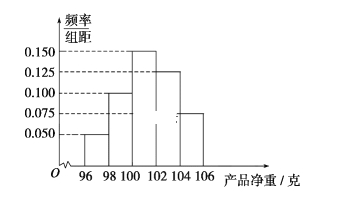
【题目】为了进一步推动全市学习型党组织、学习型社会建设,某市组织开展“学习强国”知识测试,每人测试文化、经济两个项目,每个项目满分均为60分.从全体测试人员中随机抽取了100人,分别统计他们文化、经济两个项目的测试成绩,得到文化项目测试成绩的频数分布表和经济项目测试成绩的频率分布直方图如下:
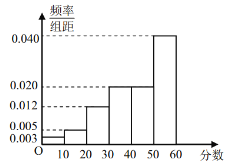
经济项目测试成绩频率分布直方图
分数区间 | 频数 |
| 2 |
| 3 |
| 5 |
| 15 |
| 40 |
| 35 |
文化项目测试成绩频数分布表
将测试人员的成绩划分为三个等级如下:分数在区间![]() 内为一般,分数在区间
内为一般,分数在区间![]() 内为良好,分数在区间
内为良好,分数在区间![]() 内为优秀.
内为优秀.
(1)在抽取的100人中,经济项目等级为优秀的测试人员中女生有14人,经济项目等级为一般或良好的测试人员中女生有34人.填写下面列联表,并根据列联表判断是否有![]() 以上的把握认为“经济项目等级为优秀”与性别有关?
以上的把握认为“经济项目等级为优秀”与性别有关?
优秀 | 一般或良好 | 合计 | |
男生数 | |||
女生数 | |||
合计 |
(2)用这100人的样本估计总体,假设这两个项目的测试成绩相互独立.
(i)从该市测试人员中随机抽取1人,估计其“文化项目等级高于经济项目等级”的概率.
(ii)对该市文化项目、经济项目的学习成绩进行评价.
附:
| 0.150 | 0.050 | 0.010 |
| 2.072 | 3.841 | 6.635 |
![]() .
.
【题目】某公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间x与乘客等候人数y之间的关系,经过调查得到如下数据:
间隔时间x/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
(1)从这6组数据中随机选取4组数据,求剩下的2组数据的间隔时间相邻的概率;
(2)若选取的是中间4组数据,求y关于x的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”.
,并判断此方程是否是“恰当回归方程”.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: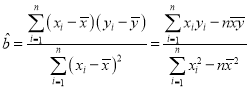 ,
,![]() .
.