题目内容
双曲线x2-my2=1的实轴长是虚轴长的2倍,则m= ( )
A. 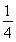 B.
B. 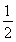 C.2 D.4
C.2 D.4
D
【解析】双曲线方程可化为x2-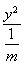 =1,∴实轴长为2,虚轴长为2
=1,∴实轴长为2,虚轴长为2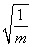 ,∴2=2
,∴2=2 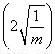 ,解得m=4.
,解得m=4.

练习册系列答案
相关题目
题目内容
双曲线x2-my2=1的实轴长是虚轴长的2倍,则m= ( )
A. 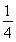 B.
B. 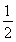 C.2 D.4
C.2 D.4
D
【解析】双曲线方程可化为x2-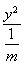 =1,∴实轴长为2,虚轴长为2
=1,∴实轴长为2,虚轴长为2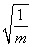 ,∴2=2
,∴2=2 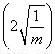 ,解得m=4.
,解得m=4.
