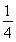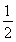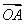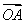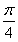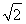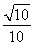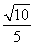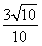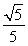题目内容
已知向量a=(cos α,sin α),b=(cos x,sin x),c=(sin x+2sin α,cos x+2cos α),其中0<α<x<π.
(1)若α= ,求函数f(x)=b·c的最小值及相应x的值;
,求函数f(x)=b·c的最小值及相应x的值;
(2)若a与b的夹角为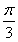 ,且a⊥c,求tan 2α的值.
,且a⊥c,求tan 2α的值.
(1)最小值为-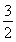 ,相应x的值为
,相应x的值为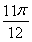 (2)-
(2)-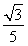
【解析】(1)∵b=(cos x,sin x),c=(sin x+2sin α,cos x+2cos α),α=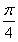 ,
,
∴f(x)=b·c=cos xsin x+2cos xsin α+sin xcos x+2sin xcos α=2sin xcos x+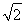 (sin x+cos x).
(sin x+cos x).
令t=sin x+cos x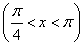 ,则2sin xcos x=t2-1,且-1<t<
,则2sin xcos x=t2-1,且-1<t<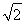 .
.
则y=t2+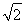 t-1=
t-1= 2-
2-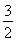 ,-1<t<
,-1<t<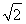 ,
,
∴t=-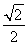 时,ymin=-
时,ymin=-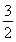 ,此时sin x+cos x=-
,此时sin x+cos x=-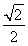 ,即
,即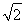 sin
sin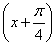 =-
=-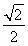 ,
,
∵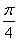 <x<π,∴
<x<π,∴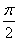 <x+
<x+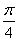 <
<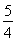 π,∴x+
π,∴x+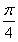 =
=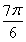 ,∴x=
,∴x=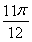 .
.
∴函数f(x)的最小值为-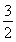 ,相应x的值为
,相应x的值为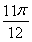 .
.
(2)∵a与b的夹角为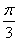 ,∴cos
,∴cos 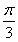 =
=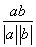 =cos αcos x+sin αsin x=cos(x-α).
=cos αcos x+sin αsin x=cos(x-α).
∵0<α<x<π,∴0<x-α<π,∴x-α=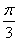 .
.
∵a⊥c,∴cos α(sin x+2sin α)+sin α(cos x+2cos α)=0,
∴sin(x+α)+2sin 2α=0,即sin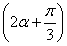 +2sin 2α=0,
+2sin 2α=0,
∴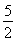 sin 2α+
sin 2α+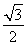 cos 2α=0,∴tan 2α=-
cos 2α=0,∴tan 2α=-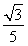 .
.

练习册系列答案
相关题目