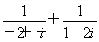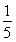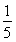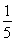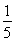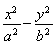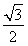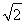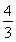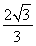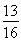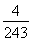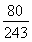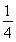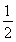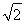题目内容
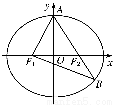
已知椭圆E: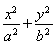 =1(a>b>0)的右焦点为F,过原点和x轴不重合的直线与椭圆E相交于A,B两点,且|AF|+|BF|=2
=1(a>b>0)的右焦点为F,过原点和x轴不重合的直线与椭圆E相交于A,B两点,且|AF|+|BF|=2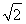 ,|AB|的最小值为2.
,|AB|的最小值为2.
(1)求椭圆E的方程;
(2)若圆x2+y2=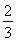 的切线L与椭圆E相交于P,Q两点,当P,Q两点横坐标不相等时,OP(O为坐标原点)与OQ是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
的切线L与椭圆E相交于P,Q两点,当P,Q两点横坐标不相等时,OP(O为坐标原点)与OQ是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
(1)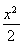 +y2=1(2)垂直
+y2=1(2)垂直
【解析】(1)设A(x0,y0),则B(-x0,-y0),F(c,0)(c2=a2-b2)
|AF|+|BF|=2a=2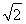 ,∴a=
,∴a=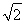 .
.
又|AB|=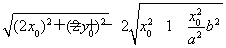 ?=2
?=2 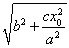 ,0≤
,0≤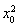 ≤a2,
≤a2,
∴|AB|min=2b=2,∴b=1,∴椭圆E的方程为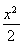 +y2=1.
+y2=1.
(2)由题设条件可知直线L的斜率存在,设直线L的方程为y=kx+m.
∵直线L与圆x2+y2=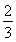 相切,∴
相切,∴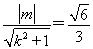 ,
,
∴m2=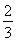 (k2+1).
(k2+1).
将y=kx+m代入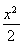 +y2=1中得,
+y2=1中得,
(1+2k2)x2+4kmx+2m2-2=0,Δ=8(2k2+1-m2)>0.
令P(x1,y1),Q(x2,y2),x1≠x2,
则x1+x2=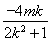 ①,x1x2=
①,x1x2=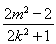 ②,
②,
y1y2=k2x1x2+km(x1+x2)+m2=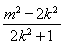 ③.
③.
∴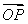 ·
·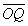 =x1x2+y1y2=
=x1x2+y1y2=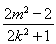 +
+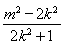 =
=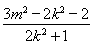 =0,
=0,
∴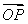 ⊥
⊥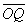 ,即OP与OQ垂直
,即OP与OQ垂直

练习册系列答案
相关题目