题目内容
函数f(x)的定义域为R,f(-2)=2,对任意x∈R,xf′(x)>-f(x),则xf(x)<-4的解集为( )
| A.(-2,2) | B.(-2,+∞) | C.(-∞,-2) | D.(-∞,+∞) |
C
构造函数g(x)=xf(x)+4,则g′(x)=xf′(x)+f(x),
∵xf′(x)>-f(x),
∴xf′(x)+f(x)>0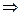 g′(x)>0
g′(x)>0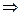 g(x)在R上单调递增.
g(x)在R上单调递增.
∵f(-2)=2,
∴g(-2)=(-2)f(-2)+4=-4+4=0.
∴x>-2时,g(x)>0; x<-2时,g(x)<0,
∴xf(x)<-4的解集为g(x)<0之解集,即x<-2.
∵xf′(x)>-f(x),
∴xf′(x)+f(x)>0
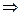 g′(x)>0
g′(x)>0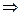 g(x)在R上单调递增.
g(x)在R上单调递增.∵f(-2)=2,
∴g(-2)=(-2)f(-2)+4=-4+4=0.
∴x>-2时,g(x)>0; x<-2时,g(x)<0,
∴xf(x)<-4的解集为g(x)<0之解集,即x<-2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
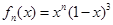 在
在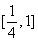 上的最大值为
上的最大值为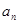 (
(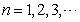 ).
).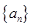 的通项公式;
的通项公式;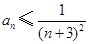 成立;
成立;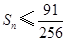 成立.
成立.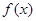 定义在
定义在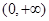 上,
上,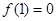 ,导函数
,导函数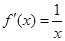 ,
, .
. 的单调区间和最小值;
的单调区间和最小值;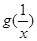 的大小关系;
的大小关系;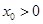 ,使得
,使得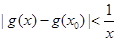 对任意
对任意 成立?若存在,求出
成立?若存在,求出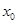 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. 与日产量
与日产量 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率
(日产品废品率
 ).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润 日正品赢利额
日正品赢利额 日废品亏损额)
日废品亏损额) (千元)表示为日产量
(千元)表示为日产量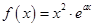 (
(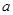 为小于
为小于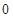 的常数).
的常数).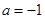 时,求函数
时,求函数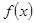 的单调区间;
的单调区间;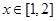 使不等式
使不等式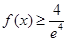 成立,求实数
成立,求实数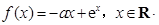
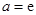 ,求函数
,求函数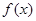 的单调区间;
的单调区间;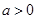 ,且对于任意
,且对于任意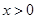 不等式
不等式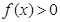 恒成立,试确定实数
恒成立,试确定实数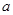 的取值范围;
的取值范围;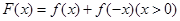 ,求证:
,求证: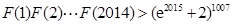
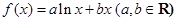 ,
,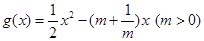 ,且
,且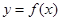 在点
在点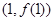 处的切线方程为
处的切线方程为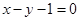 .
.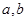 的值;
的值;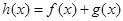 在区间
在区间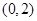 内有且仅有一个极值点,求
内有且仅有一个极值点,求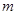 的取值范围;
的取值范围; 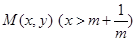 为两曲线
为两曲线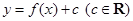 ,
,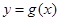 的交点,且两曲线在交点
的交点,且两曲线在交点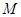 处的切线分别为
处的切线分别为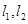 .若取
.若取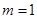 ,试判断当直线
,试判断当直线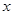 轴围成等腰三角形时
轴围成等腰三角形时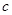 值的个数并说明理由.
值的个数并说明理由.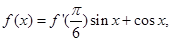 则
则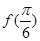 的值为 .
的值为 .