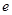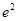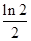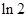题目内容
已知函数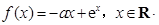
(1)若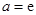 ,求函数
,求函数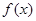 的单调区间;
的单调区间;
(2)若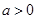 ,且对于任意
,且对于任意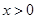 不等式
不等式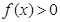 恒成立,试确定实数
恒成立,试确定实数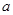 的取值范围;
的取值范围;
(3)构造函数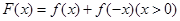 ,求证:
,求证: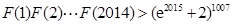
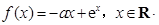
(1)若
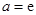 ,求函数
,求函数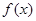 的单调区间;
的单调区间;(2)若
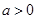 ,且对于任意
,且对于任意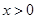 不等式
不等式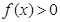 恒成立,试确定实数
恒成立,试确定实数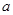 的取值范围;
的取值范围;(3)构造函数
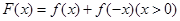 ,求证:
,求证: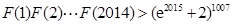
(1)若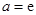 ,函数
,函数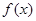 的单调递减区间是
的单调递减区间是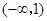 ,单调递增区间是
,单调递增区间是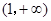 .
.
(2)若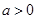 ,且对于任意
,且对于任意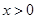 不等式
不等式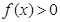 恒成立,实数
恒成立,实数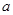 的取值范围是
的取值范围是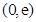 .
.
(3)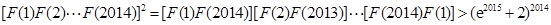 ,
,
故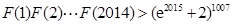 .
.
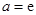 ,函数
,函数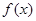 的单调递减区间是
的单调递减区间是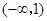 ,单调递增区间是
,单调递增区间是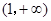 .
.(2)若
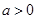 ,且对于任意
,且对于任意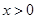 不等式
不等式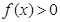 恒成立,实数
恒成立,实数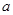 的取值范围是
的取值范围是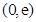 .
.(3)
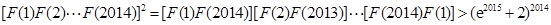 ,
,故
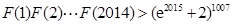 .
.解:(1)
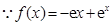 ,
,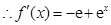 .
. 当
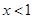 时,
时,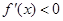 ;当
;当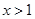 时,
时,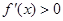 .
.因此,函数
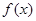 的单调递减区间是
的单调递减区间是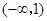 ,单调递增区间是
,单调递增区间是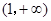 .
.(2)由
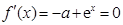 ,得
,得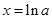 .
.当
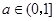 时,
时,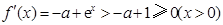 .
.此时,
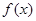 在
在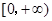 上单调递增.
上单调递增.故
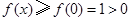 ,符合题意.
,符合题意.②当
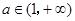 时,
时,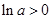 .
.当
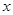 变化时,
变化时,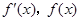 的变化情况如下表:
的变化情况如下表: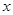 | 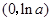 | 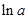 | 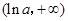 |
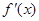 | 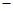 |  | 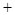 |
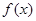 |  | 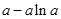 |  |
由上表可知,当
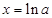 时,
时,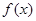 有最小值
有最小值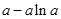 .
.依题意,得
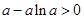 ,
,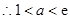 .
.综上:实数
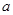 的取值范围是
的取值范围是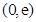 .
.(3)
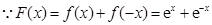 ,
,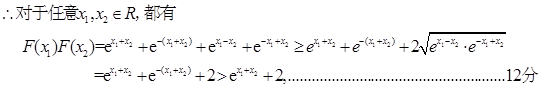
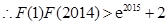 ,
,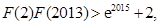
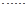 ,
,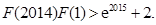
因此,
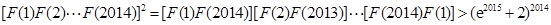 ,
,故
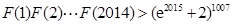 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.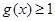 ;
;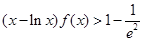 .
. ,其中
,其中 且m为常数.
且m为常数. 时函数
时函数 在区间
在区间 上的单调性,并证明;
上的单调性,并证明;  在
在 处取得极值,求
处取得极值,求 的值,并讨论函数
的值,并讨论函数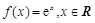 .
. 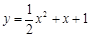 有唯一公共点.
有唯一公共点. 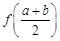 与
与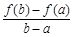 的大小, 并说明理由.
的大小, 并说明理由.  是R上的单调增函数,则
是R上的单调增函数,则 的取值范围是( )
的取值范围是( )



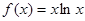 ,若
,若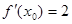 ,则
,则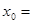 ( )
( )