题目内容
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:f′′(x)是函数y=f(x)的导数f′(x)的导数,若方程f′′(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有′拐点′;任何一个三次函数都有对称中心,且‘拐点’就是对称中心”.请你将这一发现作为条件,则函数f(x)=x3-3x2+3x的对称中心为__________.
(1,1)
f′(x)=3x2-6x+3,f′′(x)=6x-6,
令6x-6=0得x=1.
因为f(1)=1,
所以f(x)的对称中心为(1,1).
令6x-6=0得x=1.
因为f(1)=1,
所以f(x)的对称中心为(1,1).

练习册系列答案
相关题目
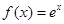 ,
,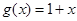 .
.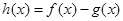 的最小值;
的最小值;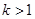 ,证明:当
,证明:当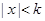 时,
时,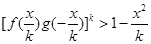 .
. 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件。
万件。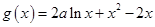 .
.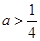 时,讨论函数
时,讨论函数 的单调性;
的单调性;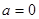 时,在函数
时,在函数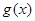 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为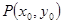 ,试探究函数
,试探究函数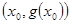 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系?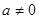 时
时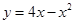 上两点
上两点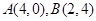 ,若曲线上一点
,若曲线上一点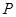 处的切线恰好平行于弦
处的切线恰好平行于弦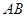 ,则点
,则点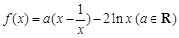 .
.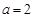 ,求曲线
,求曲线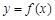 在点
在点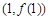 处的切线方程;
处的切线方程;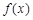 的单调区间;
的单调区间;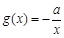 .若至少存在一个
.若至少存在一个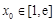 ,使得
,使得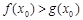 成立,求实数
成立,求实数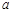 的取值范围.
的取值范围.


