题目内容
设函数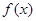 定义在
定义在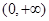 上,
上,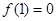 ,导函数
,导函数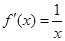 ,
, .
.
(1)求 的单调区间和最小值;
的单调区间和最小值;
(2)讨论 与
与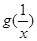 的大小关系;
的大小关系;
(3)是否存在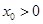 ,使得
,使得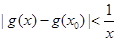 对任意
对任意 成立?若存在,求出
成立?若存在,求出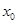 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
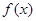 定义在
定义在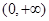 上,
上,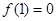 ,导函数
,导函数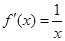 ,
, .
.(1)求
 的单调区间和最小值;
的单调区间和最小值;(2)讨论
 与
与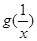 的大小关系;
的大小关系;(3)是否存在
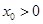 ,使得
,使得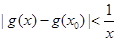 对任意
对任意 成立?若存在,求出
成立?若存在,求出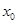 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.(1)区间在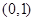 是函数
是函数 的减区间;区间在
的减区间;区间在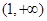 是函数
是函数 的增区间;最小值是
的增区间;最小值是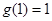
(2)当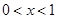 时,
时,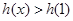 =0,∴
=0,∴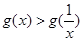 ;
;
当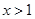 时,
时,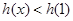 =0,∴
=0,∴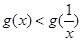 .
.
(3)不存在,见解析
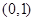 是函数
是函数 的减区间;区间在
的减区间;区间在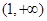 是函数
是函数 的增区间;最小值是
的增区间;最小值是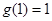
(2)当
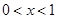 时,
时,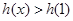 =0,∴
=0,∴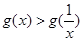 ;
;当
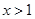 时,
时,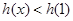 =0,∴
=0,∴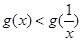 .
.(3)不存在,见解析
(1)先求出原函数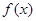 ,再求得
,再求得 ,然后利用导数判断函数的单调性(单调区间),并求出最小值;(2)作差法比较,构造一个新的函数,利用导数判断函数的单调性,并由单调性判断函数的正负;(3)存在性问题通常采用假设存在,然后进行求解;注意利用前两问的结论.
,然后利用导数判断函数的单调性(单调区间),并求出最小值;(2)作差法比较,构造一个新的函数,利用导数判断函数的单调性,并由单调性判断函数的正负;(3)存在性问题通常采用假设存在,然后进行求解;注意利用前两问的结论.
(1)∵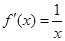 ,∴
,∴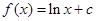 (
(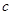 为常数),又∵
为常数),又∵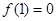 ,所以
,所以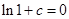 ,即
,即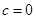 ,
,
∴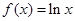 ;
;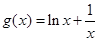 ,
,
∴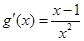 ,令
,令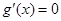 ,即
,即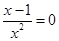 ,解得
,解得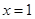 ,
,
当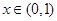 时,
时,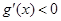 ,
, 是减函数,故区间在
是减函数,故区间在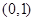 是函数
是函数 的减区间;
的减区间;
当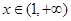 时,
时,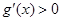 ,
, 是增函数,故区间在
是增函数,故区间在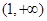 是函数
是函数 的增区间;
的增区间;
所以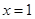 是
是 的唯一极值点,且为极小值点,从而是最小值点,
的唯一极值点,且为极小值点,从而是最小值点,
所以 的最小值是
的最小值是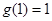 .
.
(2)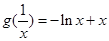 ,设
,设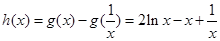 ,
,
则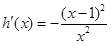 ,
,
当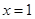 时,
时,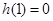 ,即
,即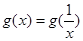 ,
,
当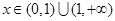 时,
时,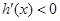 ,
,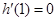 ,
,
因此函数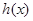 在
在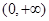 内单调递减,
内单调递减,
当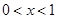 时,
时,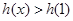 =0,∴
=0,∴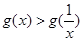 ;
;
当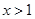 时,
时,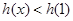 =0,∴
=0,∴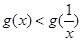 .
.
(3)满足条件的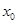 不存在.证明如下:
不存在.证明如下:
证法一 假设存在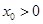 ,使
,使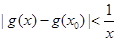 对任意
对任意 成立,
成立,
即对任意 有
有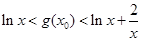 ①
①
但对上述的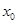 ,取
,取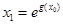 时,有
时,有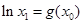 ,这与①左边的不等式矛盾,
,这与①左边的不等式矛盾,
因此不存在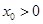 ,使
,使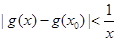 对任意
对任意 成立.
成立.
证法二 假设存在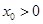 ,使
,使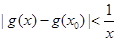 对任意
对任意 成立,
成立,
由(1)知, 的最小值是
的最小值是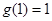 ,
,
又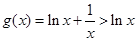 ,而
,而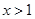 时,
时,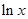 的值域为
的值域为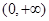 ,
,
∴当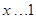 时,
时, 的值域为
的值域为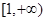 ,
,
从而可以取一个值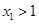 ,使
,使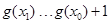 ,即
,即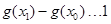 ,
,
∴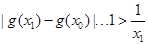 ,这与假设矛盾.
,这与假设矛盾.
∴不存在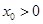 ,使
,使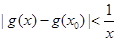 对任意
对任意 成立.
成立.
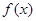 ,再求得
,再求得 ,然后利用导数判断函数的单调性(单调区间),并求出最小值;(2)作差法比较,构造一个新的函数,利用导数判断函数的单调性,并由单调性判断函数的正负;(3)存在性问题通常采用假设存在,然后进行求解;注意利用前两问的结论.
,然后利用导数判断函数的单调性(单调区间),并求出最小值;(2)作差法比较,构造一个新的函数,利用导数判断函数的单调性,并由单调性判断函数的正负;(3)存在性问题通常采用假设存在,然后进行求解;注意利用前两问的结论.(1)∵
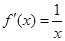 ,∴
,∴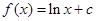 (
(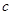 为常数),又∵
为常数),又∵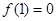 ,所以
,所以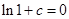 ,即
,即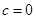 ,
,∴
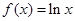 ;
;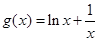 ,
,∴
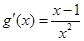 ,令
,令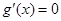 ,即
,即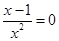 ,解得
,解得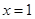 ,
,当
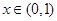 时,
时,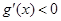 ,
, 是减函数,故区间在
是减函数,故区间在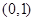 是函数
是函数 的减区间;
的减区间;当
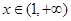 时,
时,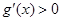 ,
, 是增函数,故区间在
是增函数,故区间在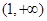 是函数
是函数 的增区间;
的增区间;所以
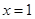 是
是 的唯一极值点,且为极小值点,从而是最小值点,
的唯一极值点,且为极小值点,从而是最小值点,所以
 的最小值是
的最小值是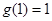 .
.(2)
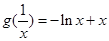 ,设
,设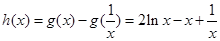 ,
,则
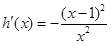 ,
,当
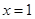 时,
时,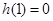 ,即
,即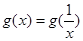 ,
,当
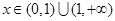 时,
时,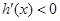 ,
,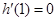 ,
,因此函数
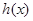 在
在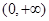 内单调递减,
内单调递减,当
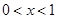 时,
时,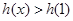 =0,∴
=0,∴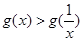 ;
;当
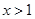 时,
时,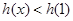 =0,∴
=0,∴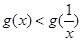 .
. (3)满足条件的
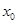 不存在.证明如下:
不存在.证明如下:证法一 假设存在
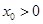 ,使
,使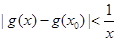 对任意
对任意 成立,
成立,即对任意
 有
有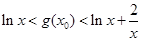 ①
①但对上述的
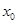 ,取
,取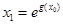 时,有
时,有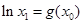 ,这与①左边的不等式矛盾,
,这与①左边的不等式矛盾,因此不存在
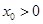 ,使
,使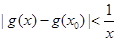 对任意
对任意 成立.
成立.证法二 假设存在
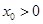 ,使
,使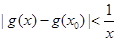 对任意
对任意 成立,
成立,由(1)知,
 的最小值是
的最小值是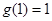 ,
,又
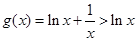 ,而
,而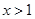 时,
时,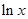 的值域为
的值域为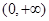 ,
,∴当
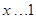 时,
时, 的值域为
的值域为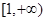 ,
,从而可以取一个值
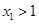 ,使
,使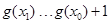 ,即
,即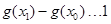 ,
,∴
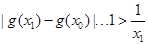 ,这与假设矛盾.
,这与假设矛盾.∴不存在
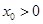 ,使
,使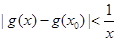 对任意
对任意 成立.
成立.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,其中
,其中 且m为常数.
且m为常数. 时函数
时函数 在区间
在区间 上的单调性,并证明;
上的单调性,并证明;  在
在 处取得极值,求
处取得极值,求 的值,并讨论函数
的值,并讨论函数 .
. 的单调性;
的单调性;  ,求
,求 上的最大值;
上的最大值; ,不等式
,不等式 都成立(其中
都成立(其中 是自然对数的底数).
是自然对数的底数).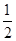 x2+2xf′(2014)+2014lnx,则f′(2014)=( )
x2+2xf′(2014)+2014lnx,则f′(2014)=( )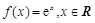 .
. 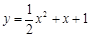 有唯一公共点.
有唯一公共点. 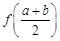 与
与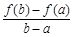 的大小, 并说明理由.
的大小, 并说明理由. 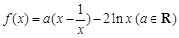 .
.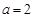 ,求曲线
,求曲线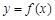 在点
在点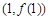 处的切线方程;
处的切线方程;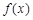 的单调区间;
的单调区间;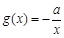 .若至少存在一个
.若至少存在一个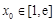 ,使得
,使得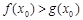 成立,求实数
成立,求实数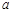 的取值范围.
的取值范围. ,要得到
,要得到 f′(x)的图象,只需将f(x)的图象( )个单位.
f′(x)的图象,只需将f(x)的图象( )个单位.




