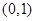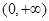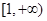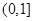题目内容
已知f(x)与g(x)是定义在R上的非奇非偶函数，且h(x)=f(x)g(x)是定义在R上的偶函数，试写出满足条件的一组函数：f(x)= ，g(x)= （只要写出满足条件的一组即可）
x+1，x－1
已知f（x）与g（x）是定义在R上的非奇非偶函数，且h（x）=f（x）g（x）是定义在R上的偶函数，可以令f（x）=x+1，g（x）=x-1，从而求解；
解：∵f（x）与g（x）是定义在R上的非奇非偶函数，且h（x）=f（x）g（x）是定义在R上的偶函数，
∴可以找f（x）=x+1，g（x）=x-1，构成平方差公式，
h（x）=f（x）g（x）=x2-1，h（x）为偶函数，
故答案为：f（x）=x+1，g（x）=x-1；（答案不唯一）
解：∵f（x）与g（x）是定义在R上的非奇非偶函数，且h（x）=f（x）g（x）是定义在R上的偶函数，
∴可以找f（x）=x+1，g（x）=x-1，构成平方差公式，
h（x）=f（x）g（x）=x2-1，h（x）为偶函数，
故答案为：f（x）=x+1，g（x）=x-1；（答案不唯一）
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
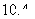
，那么经过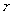
年可增长到原来的
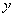倍，则函数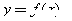
的图象大致是（ ）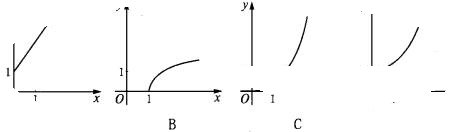 
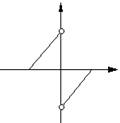
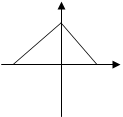
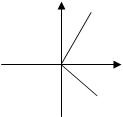
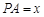，过点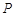
且与AB垂直的截面面积记为y，则
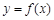的图像是（ ）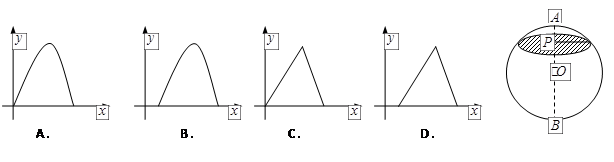
＝
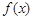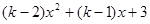是偶函数，则
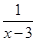； (3)A＝(0，+∞)，B＝{y|y≠0}，对应法则f：x→y＝±
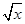；(4)A＝N*，B＝{－1，1}，对应法则f：x→y＝(－1)x 其中是函数的有 ．（只填写序号）
，
）内为减函数的是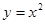
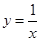
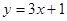
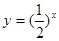
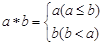，如
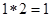，则函数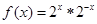
的值域为（ ）
