题目内容
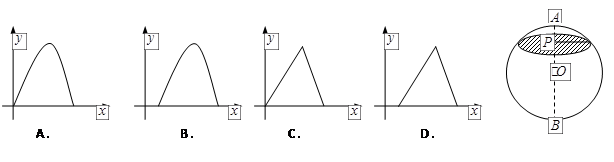
如图，点p是球O的直径AB上的动点，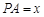
，过点
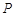且与AB垂直的截面面积记为y，则
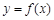的图像是（ ）
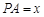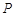，过点且与AB垂直的截面面积记为y，则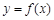的图像是（ ）A
解：设球的半径是R，截面圆的半径为r，
则在直角三角形中根据射影定理可以得到r2=x（2R-x）．
∴f（x）=πr2=π?x（2R-x）．
∴y=f（x）=-π（x-R）2+πR2．
∵把（0，0）点代入，函数成立，
∴图象是过原点且开口向下的抛物线的一部分．
故选A．
则在直角三角形中根据射影定理可以得到r2=x（2R-x）．
∴f（x）=πr2=π?x（2R-x）．
∴y=f（x）=-π（x-R）2+πR2．
∵把（0，0）点代入，函数成立，
∴图象是过原点且开口向下的抛物线的一部分．
故选A．
练习册系列答案
相关题目
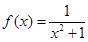，令
。
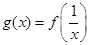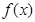的值域；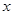
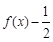
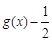
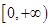的图像，请据此在该坐标系中补全函数
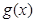的图像. 请说明你的作图依据.
满足下列条件：在定义域内存在
使得
成立，则称函数
；反之，若
不存在，则称函数
具有性质
具有性质
的取值范围；
、②
、③
、④
、⑤
的函数，指出哪些函数一定具有性质
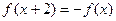，当
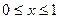时，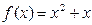
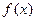的周期 （2）求函数
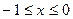的表达式 （3）求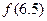
的定义域为（ ）
］
，曲线
在点
处的切线方程为
，则
等于（ ）
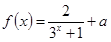的零点为1，则实数a的值为（ ）
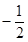C．
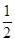D．2