题目内容
设函数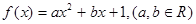 。
。
(Ⅰ)若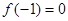 且对任意实数
且对任意实数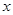 均有
均有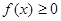 成立,求
成立,求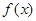 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当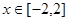 时,
时,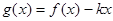 是单调函数,求实数
是单调函数,求实数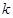 的取值范围.
的取值范围.
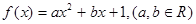 。
。(Ⅰ)若
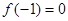 且对任意实数
且对任意实数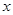 均有
均有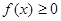 成立,求
成立,求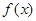 的表达式;
的表达式;(Ⅱ)在(Ⅰ)的条件下,当
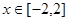 时,
时,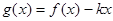 是单调函数,求实数
是单调函数,求实数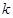 的取值范围.
的取值范围.(Ⅰ) ,(Ⅱ)
,(Ⅱ)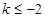 或
或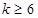
 ,(Ⅱ)
,(Ⅱ)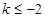 或
或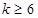
试题分析:(Ⅰ)根据
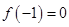 得出a,b关系,再
得出a,b关系,再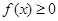 在定义域上恒成立,可得a,b的值,从而得出
在定义域上恒成立,可得a,b的值,从而得出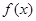 表达式.
表达式.(Ⅱ)由(Ⅰ)可推出
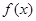 表达式,又
表达式,又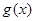 为单调函数,利用二次函数性质求得实数
为单调函数,利用二次函数性质求得实数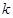 的取值范围.
的取值范围.试题解析:(Ⅰ)
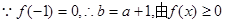 恒成立,
恒成立,知
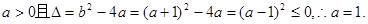
从而
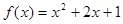 .(6分)
.(6分)(Ⅱ)由(1)可知
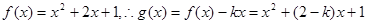 ,
,由于
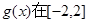 是单调函数,
是单调函数,知
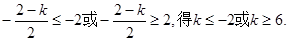 .(12分)
.(12分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
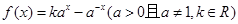 ,
,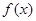 是定义域为
是定义域为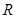 的奇函数.
的奇函数.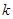 的值,判断并证明当
的值,判断并证明当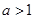 时,函数
时,函数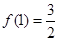 ,函数
,函数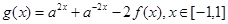 ,求
,求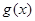 的值域;
的值域;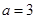 ,若
,若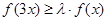 对于
对于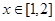 时恒成立.请求出最大的整数
时恒成立.请求出最大的整数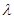 .
. 对任意实数
对任意实数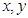 均有
均有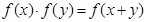 ,且当
,且当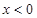 时
时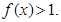
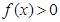 ;
;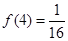 时, 对
时, 对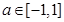 恒有
恒有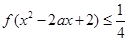 ,求实数
,求实数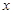 的取值范围.
的取值范围.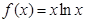 .
.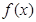 的单调区间和极值;
的单调区间和极值;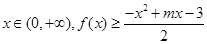 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.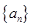 是首项为a,公差为1的等差数列,
是首项为a,公差为1的等差数列,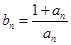 .若对任意的
.若对任意的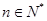 ,都有
,都有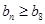 成立,则实数a的取值范围是 .
成立,则实数a的取值范围是 .
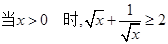
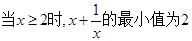
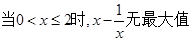
 ,则当
,则当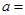 ______时,
______时, 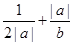 取得最小值.
取得最小值. 上的奇函数
上的奇函数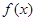 ,满足
,满足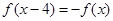 ,且在区间
,且在区间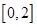 上是增函数,若方程
上是增函数,若方程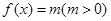 ,在区间
,在区间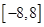 上有四个不同的根
上有四个不同的根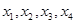 ,则
,则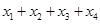 =( )
=( )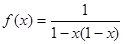 的最大值是 .
的最大值是 .