题目内容
设函数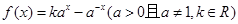 ,
,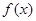 是定义域为
是定义域为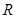 的奇函数.
的奇函数.
(Ⅰ)求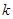 的值,判断并证明当
的值,判断并证明当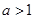 时,函数
时,函数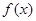 在
在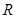 上的单调性;
上的单调性;
(Ⅱ)已知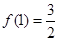 ,函数
,函数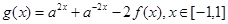 ,求
,求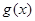 的值域;
的值域;
(Ⅲ)已知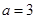 ,若
,若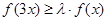 对于
对于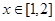 时恒成立.请求出最大的整数
时恒成立.请求出最大的整数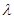 .
.
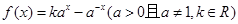 ,
,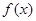 是定义域为
是定义域为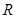 的奇函数.
的奇函数.(Ⅰ)求
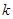 的值,判断并证明当
的值,判断并证明当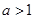 时,函数
时,函数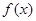 在
在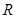 上的单调性;
上的单调性;(Ⅱ)已知
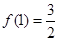 ,函数
,函数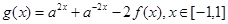 ,求
,求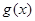 的值域;
的值域;(Ⅲ)已知
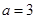 ,若
,若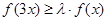 对于
对于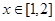 时恒成立.请求出最大的整数
时恒成立.请求出最大的整数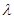 .
.(Ⅰ)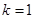 ,
,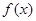 在R上为增函数;(Ⅱ)
在R上为增函数;(Ⅱ)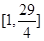 ;(Ⅲ)
;(Ⅲ)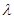 的最大整数为10.
的最大整数为10.
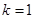 ,
,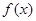 在R上为增函数;(Ⅱ)
在R上为增函数;(Ⅱ)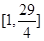 ;(Ⅲ)
;(Ⅲ)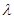 的最大整数为10.
的最大整数为10.试题分析:(Ⅰ)由奇函数的性质
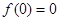 得
得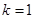 ,由单调性的定义证明
,由单调性的定义证明 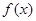 在R上是增函数;
在R上是增函数;(Ⅱ)由
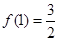 可得
可得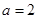 ,
,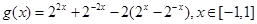 ,由换元法令
,由换元法令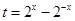 ,将函数转化为二次函数
,将函数转化为二次函数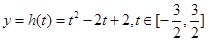 求最值;(Ⅲ)
求最值;(Ⅲ)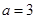 时,原式可化为
时,原式可化为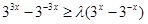 ,令
,令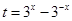 ,由分离参数的方法得到
,由分离参数的方法得到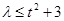 ,进而得到
,进而得到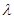 的取值范围.本题中用到换元法,换元之后应特别注意变元
的取值范围.本题中用到换元法,换元之后应特别注意变元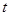 的取值范围.
的取值范围.试题解析:(Ⅰ)
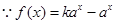 是定义域为R上的奇函数,
是定义域为R上的奇函数,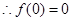 ,得
,得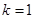 .
.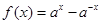 ,
,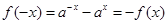 ,即
,即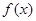 是R上的奇函数 2分
是R上的奇函数 2分设
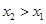 ,则
,则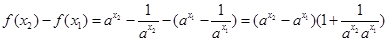 ,
,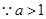 ,
,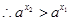 ,
,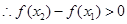 ,
,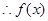 在R上为增函数 5分
在R上为增函数 5分(Ⅱ)
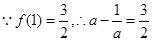 ,即
,即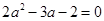 ,
,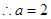 或
或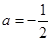 (舍去)
(舍去)则
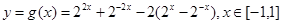 ,令
,令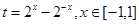 ,
,由(1)可知该函数在区间
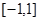 上为增函数,则
上为增函数,则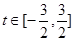
则
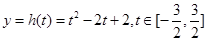 8分
8分当
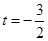 时,
时,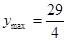 ;当
;当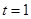 时,
时,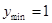
所以
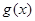 的值域为
的值域为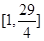 10分
10分(Ⅲ)由题意,即
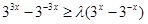 ,在
,在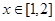 时恒成立
时恒成立令
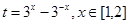 ,则
,则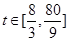
则
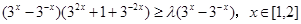 恒成立
恒成立即为
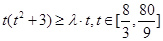 恒成立 13分
恒成立 13分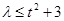 ,
,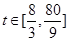 恒成立,当
恒成立,当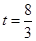 时,
时,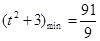
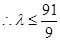 ,则
,则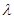 的最大整数为10 16分
的最大整数为10 16分
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
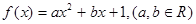 。
。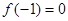 且对任意实数
且对任意实数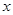 均有
均有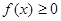 成立,求
成立,求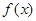 的表达式;
的表达式;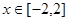 时,
时,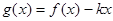 是单调函数,求实数
是单调函数,求实数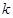 的取值范围.
的取值范围.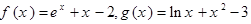 ,若实数
,若实数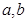 满足
满足 ,则( )
,则( )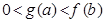
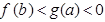
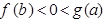
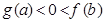
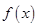 是
是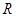 上的减函数,且
上的减函数,且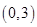 和
和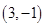 ,则不等式
,则不等式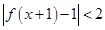 的解集是( )
的解集是( )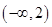
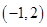
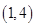
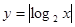 的单调递减区间是 .
的单调递减区间是 .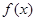 在区间
在区间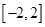 上单调递减,则不等式
上单调递减,则不等式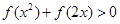 的解集是( )
的解集是( )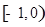
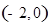
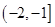

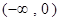 上单调递增的是 ( )
上单调递增的是 ( )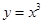
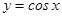
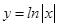
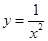
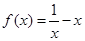 的图像关于 ( )
的图像关于 ( )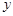 轴对称
轴对称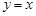
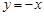
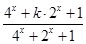 ,若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是 .
,若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是 .