题目内容
已知圆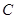 过定点
过定点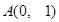 ,圆心
,圆心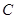 在抛物线
在抛物线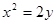 上,
上,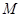 、
、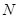 为圆
为圆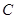 与
与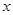 轴的交点.
轴的交点.
(1)当圆心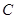 是抛物线的顶点时,求抛物线准线被该圆截得的弦长.
是抛物线的顶点时,求抛物线准线被该圆截得的弦长.
(2)当圆心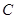 在抛物线上运动时,
在抛物线上运动时,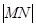 是否为一定值?请证明你的结论.
是否为一定值?请证明你的结论.
(3)当圆心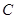 在抛物线上运动时,记
在抛物线上运动时,记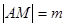 ,
,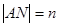 ,求
,求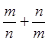 的最大值,并求出此时圆
的最大值,并求出此时圆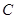 的方程.
的方程.
(1)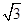 ;(2)是定值,为2;(3)
;(2)是定值,为2;(3)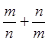 取得最大值
取得最大值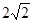 ,此时圆
,此时圆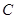 的方程为
的方程为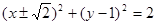 .
.
解析试题分析:(1)这是关于圆的基本计算问题,圆心是抛物线的顶点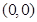 ,又圆过点
,又圆过点 ,可得圆半径为
,可得圆半径为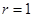 ,就得出了圆的方程,抛物线的准线为
,就得出了圆的方程,抛物线的准线为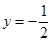 ,与圆相交弦长可用直角三角形法求解,弦心距,弦的一半,相应半径可构成一个直角三角形,应用勾股定理易得;(2)圆心在抛物线上运动,可设圆心坐标为
,与圆相交弦长可用直角三角形法求解,弦心距,弦的一半,相应半径可构成一个直角三角形,应用勾股定理易得;(2)圆心在抛物线上运动,可设圆心坐标为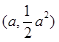 ,与(1)同法可得弦长
,与(1)同法可得弦长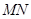 ,当然本题中弦在
,当然本题中弦在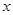 轴上,故可在圆方程中令
轴上,故可在圆方程中令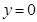 ,求出
,求出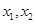 ,也即求出
,也即求出
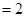 为定值;(3)根据圆的性质,由(2)可得
为定值;(3)根据圆的性质,由(2)可得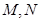 两点的坐标为
两点的坐标为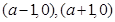 ,这样
,这样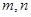 就可用
就可用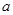 来表示,可求得
来表示,可求得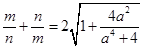 ,
, 时,有
时,有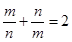 ,
,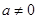 时,利用基本不等式有
时,利用基本不等式有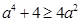 ,从而
,从而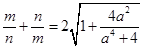
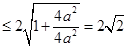 (当且仅当
(当且仅当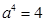 ,即
,即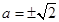 时等号成立),故所求最大值为
时等号成立),故所求最大值为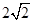 .
.
试题解析:(1)抛物线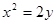 的顶点为
的顶点为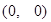 ,准线方程为
,准线方程为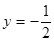 ,圆的半径等于1,圆
,圆的半径等于1,圆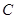 的方程为
的方程为 .弦长
.弦长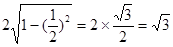 4分
4分
(2)设圆心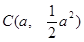 ,则圆
,则圆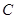 的半径
的半径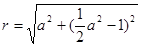 ,
,
圆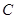 的方程是为:
的方程是为: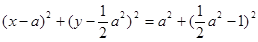 6分
6分
令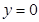 ,得
,得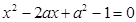 ,得
,得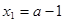 ,
,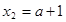 ,
,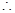
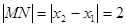 是定值. 8分
是定值. 8分
(3)由(2)知,不妨设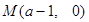 ,
,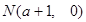 ,
,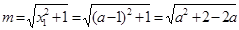 ,
,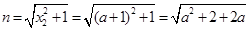 .
.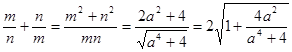 . 11分
. 11分
当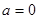 时,
时,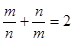 . 12分
. 12分
当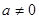 时,
时,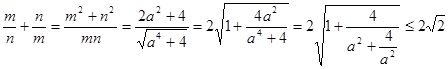 .
.
当且仅当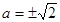 时,等号成立 14分
时,等号成立 14分
所以当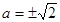 时,
时,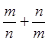 取得最大值
取得最大值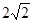 ,此时圆
,此时圆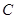 的方程为
的方程为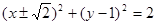 .
.
16分
考点:(1)抛物线的几何性质,圆的弦长公式;(2)圆的弦长;(3)基本不等式与最大值问题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
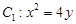 在点
在点 ,
, 处的切线垂直相交于点
处的切线垂直相交于点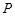 ,直线
,直线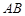 与椭圆
与椭圆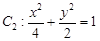 相交于
相交于 ,
,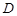 两点.
两点.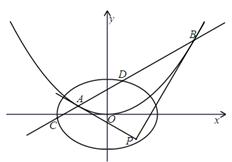
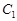 的焦点
的焦点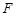 与椭圆
与椭圆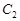 的左焦点
的左焦点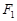 的距离;
的距离;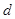 ,试问:是否存在直线
,试问:是否存在直线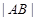 ,
,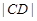 成等比数列?若存在,求直线
成等比数列?若存在,求直线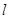 与椭圆E相交于P,Q两点,且
与椭圆E相交于P,Q两点,且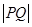 的最大值为
的最大值为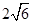 .
.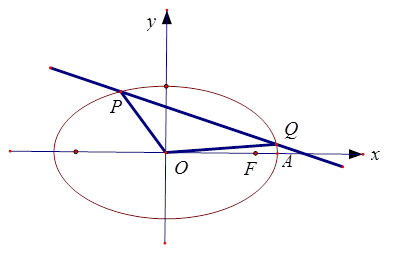
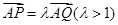 ,过点P且平行于y轴的直线与椭圆E相交于另一点M,试问M,F,Q是否共线,若共线请证明;反之说明理由.
,过点P且平行于y轴的直线与椭圆E相交于另一点M,试问M,F,Q是否共线,若共线请证明;反之说明理由. 中,已知抛物线
中,已知抛物线 ,设点
,设点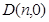 ,
,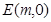 ,
,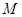 为抛物线
为抛物线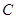 上的动点(异于顶点),连结
上的动点(异于顶点),连结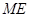 并延长交抛物线
并延长交抛物线 ,连结
,连结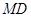 、
、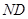 并分别延长交抛物线
并分别延长交抛物线 、
、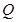 ,连结
,连结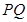 ,设
,设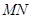 、
、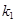 、
、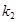 .
.
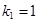 ,
,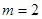 ,
,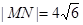 ,求
,求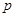 ;
;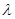 ,是的
,是的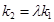 恒成立,若存在,请将
恒成立,若存在,请将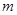 、
、 表示出来;若不存在请说明理由.
表示出来;若不存在请说明理由. ,
, ,动点
,动点 满足
满足 .
. 的方程;
的方程; :
: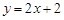 上取一点
上取一点 ,过点
,过点 .问:是否存在点
.问:是否存在点 //
//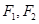 是椭圆E:
是椭圆E: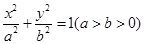 的两个焦点,抛物线
的两个焦点,抛物线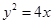 的焦点为椭圆E的一个焦点,直线y=
的焦点为椭圆E的一个焦点,直线y=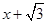 上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,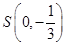 的动直线
的动直线 交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由。
交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由。
 :
: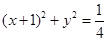 ,
,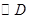 :
: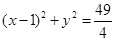 .动点P与
.动点P与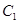 的方程;
的方程;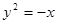 与直线
与直线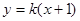 相交于A、B 两点.
相交于A、B 两点.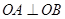 ;
;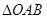 的面积等于
的面积等于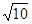 时,求
时,求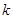 的值.
的值.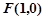 ,点
,点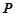 是点
是点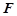 关于
关于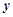 轴的对称点,过点
轴的对称点,过点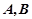 两点。
两点。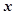 轴上是否存在不同于点
轴上是否存在不同于点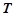 ,使得
,使得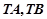 与
与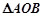 的面积为
的面积为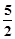 ,求向量
,求向量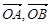 的夹角;
的夹角;