题目内容
抛物线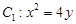 在点
在点 ,
, 处的切线垂直相交于点
处的切线垂直相交于点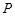 ,直线
,直线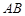 与椭圆
与椭圆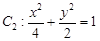 相交于
相交于 ,
, 两点.
两点.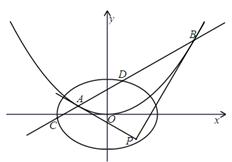
(1)求抛物线 的焦点
的焦点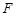 与椭圆
与椭圆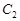 的左焦点
的左焦点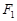 的距离;
的距离;
(2)设点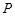 到直线
到直线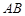 的距离为
的距离为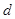 ,试问:是否存在直线
,试问:是否存在直线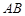 ,使得
,使得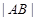 ,
,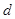 ,
,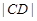 成等比数列?若存在,求直线
成等比数列?若存在,求直线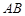 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(1)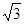 ;(2)不存在.
;(2)不存在.
解析试题分析:(1)分别求出抛物线与椭圆的焦点,利用两点间距离公式求解;(2)设直线 与抛物线相交于
与抛物线相交于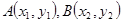 与椭圆相交于
与椭圆相交于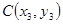 ,
,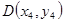 ,所以直线与抛物线方程联立,得到
,所以直线与抛物线方程联立,得到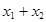 和
和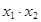 然后利用
然后利用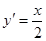 ,求出切线
,求出切线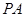 ,
,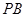 的斜率,利用切线垂直,
的斜率,利用切线垂直,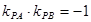 ,解出m,然后分别设出过
,解出m,然后分别设出过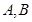 点的切线方程,求出交点
点的切线方程,求出交点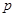 的坐标,利用点到直线的距离公式求
的坐标,利用点到直线的距离公式求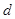 ,直线与曲线相交的弦长公式求
,直线与曲线相交的弦长公式求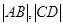 ,若
,若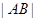 ,
,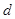 ,
,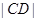 成等比数列,则
成等比数列,则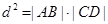 ,化简等式,通过
,化简等式,通过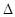 看方程实根情况.
看方程实根情况.
试题解析:(I)抛物线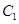 的焦点
的焦点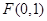 , 1分
, 1分
椭圆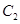 的左焦点
的左焦点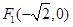 , 2分
, 2分
则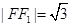 . 3分
. 3分
(II)设直线 ,
,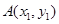 ,
, ,
,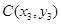 ,
,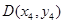 ,
,
由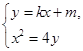 ,得
,得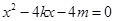 , 4分
, 4分
故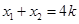 ,
,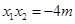 .
.
由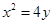 ,得
,得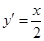 ,
,
故切线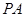 ,
,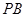 的斜率分别为
的斜率分别为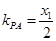 ,
,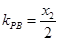 ,
,
再由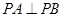 ,得
,得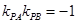 ,
,
即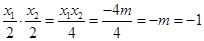 ,
,
故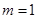 ,这说明直线
,这说明直线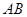 过抛物线
过抛物线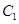 的焦点
的焦点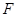 . 7分
. 7分
由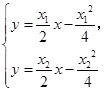 ,得
,得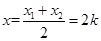 ,
,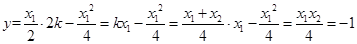 ,即
,即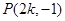 . 8分
. 8分
于是点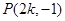 到直线
到直线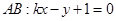 的距离
的距离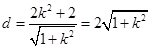 . 9分
. 9分
由 ,得
,得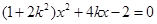 , 10分
, 10分
从而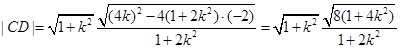 , 11分
, 11分
同理,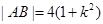 . 12分
. 12分
若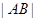 ,
,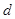 ,
,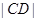 成等比数列,则
成等比数列,则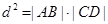 , 13分
, 13分
即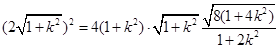 ,
,
化简整理,得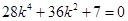 ,此方程无实根,
,此方程无实根,
所以不存在直线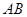 ,使得
,使得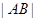 ,
,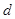 ,
,
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
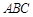 的两个顶点
的两个顶点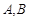 的坐标分别是
的坐标分别是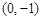 ,
,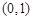 ,且
,且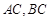 所在直线的斜率之积等于
所在直线的斜率之积等于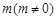 .
.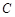 的轨迹
的轨迹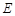 的方程,并判断轨迹
的方程,并判断轨迹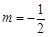 时,过点
时,过点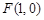 的直线
的直线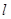 交曲线
交曲线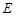 于
于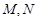 两点,设点
两点,设点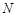 关于
关于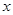 轴的对称点为
轴的对称点为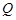 (
(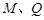 不重合), 试问:直线
不重合), 试问:直线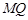 与
与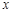 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.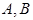 是椭圆
是椭圆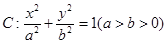 的左、右顶点,椭圆
的左、右顶点,椭圆 的离心率为
的离心率为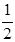 ,右准线
,右准线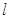 的方程为
的方程为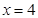 .
.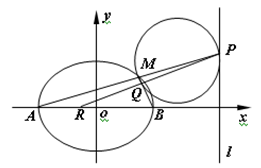
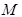 是椭圆
是椭圆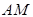 交
交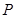 ,以
,以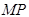 为直径的圆记为
为直径的圆记为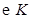 . ①若
. ①若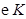 截直线
截直线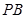 所得的弦长;
所得的弦长;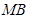 交于点
交于点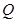 ,试证明:直线
,试证明:直线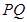 与
与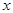 轴的交点
轴的交点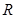 为定点,并求该定点的坐标.
为定点,并求该定点的坐标.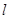 与椭圆
与椭圆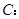
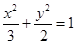 交于
交于
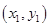 、
、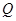
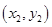 两不同点,且△
两不同点,且△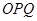 的面积
的面积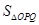 =
=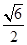 ,其中
,其中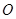 为坐标原点.
为坐标原点.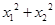 和
和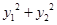 均为定值;
均为定值;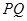 的中点为
的中点为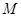 ,求
,求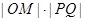 的最大值;
的最大值;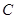 上是否存在点
上是否存在点 ,使得
,使得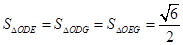 ?若存在,判断△
?若存在,判断△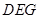 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由.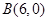 和
和 ,过点
,过点 的直线
的直线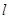 与过点
与过点 的直线
的直线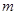 相交于点
相交于点 ,设直线
,设直线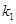 ,直线
,直线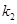 ,如果
,如果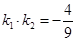 ,求点
,求点 中,
中,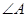 的外角平分线
的外角平分线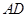 与边
与边 的延长线相交于点
的延长线相交于点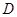 ,则
,则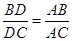 .
.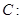
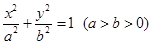 的左、右焦点分别为
的左、右焦点分别为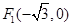 、
、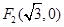 ,椭圆上的点
,椭圆上的点 满足
满足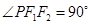 ,且
,且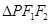 的面积
的面积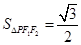 .
.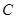 的方程;
的方程;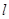 ,使
,使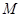 、
、 ,且线段
,且线段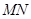 恰被直线
恰被直线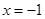 平分?若存在,求出
平分?若存在,求出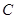 过定点
过定点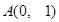 ,圆心
,圆心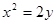 上,
上,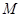 、
、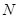 为圆
为圆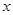 轴的交点.
轴的交点.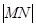 是否为一定值?请证明你的结论.
是否为一定值?请证明你的结论.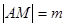 ,
,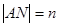 ,求
,求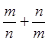 的最大值,并求出此时圆
的最大值,并求出此时圆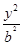 =1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
=1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.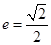 的椭圆
的椭圆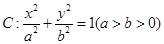 一个焦点为
一个焦点为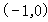 .
. 的方程;
的方程; 交椭圆
交椭圆 两点,且
两点,且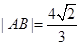 ,求直线
,求直线