题目内容
(本题满分12分)
已知函数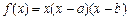 .
.
(Ⅰ)若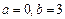 ,函数
,函数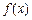 在
在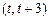 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求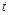 的取值范围;
的取值范围;
(Ⅱ)当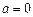 时,
时,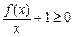 对
对 任意的
任意的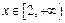 恒成立,求
恒成立,求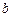 的取值范围.
的取值范围.
已知函数
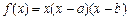 .
.(Ⅰ)若
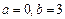 ,函数
,函数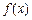 在
在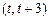 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求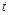 的取值范围;
的取值范围;(Ⅱ)当
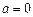 时,
时,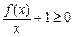 对
对 任意的
任意的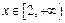 恒成立,求
恒成立,求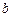 的取值范围.
的取值范围.解:(Ⅰ)当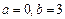 时,
时,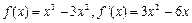 ,
,
令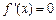 得
得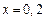 ,根据导数的符号可以得出函数
,根据导数的符号可以得出函数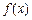 在
在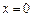 处取得极大值,
处取得极大值,
在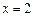 处取得极小值.函数
处取得极小值.函数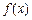 在
在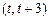 上既能取到极大值,又能取到极小值,
上既能取到极大值,又能取到极小值,
则只要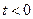 且
且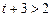 即可,即只要
即可,即只要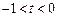 即可.
即可.
所以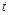 的取值范围是
的取值范围是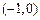 .
.  ……………5分
……………5分
(Ⅱ)当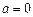 时,
时,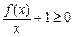 对任意的
对任意的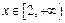 恒成立,
恒成立,
即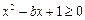 对任意的
对任意的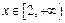 恒成立,
恒成立,
也即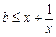 在对任意的
在对任意的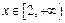 恒成立. ……………7分
恒成立. ……………7分
令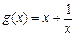 ,则
,则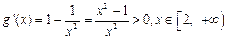 .
.
则函数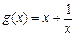 在
在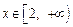 上单调递增,
上单调递增,
当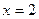 时取最小值
时取最小值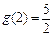 ,故只要
,故只要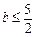 即可.
即可.
所以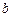 的取值范围是
的取值范围是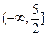 . ……………12分
. ……………12分
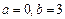 时,
时,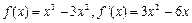 ,
,令
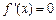 得
得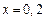 ,根据导数的符号可以得出函数
,根据导数的符号可以得出函数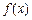 在
在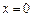 处取得极大值,
处取得极大值,在
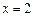 处取得极小值.函数
处取得极小值.函数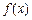 在
在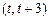 上既能取到极大值,又能取到极小值,
上既能取到极大值,又能取到极小值,则只要
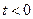 且
且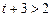 即可,即只要
即可,即只要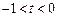 即可.
即可.所以
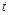 的取值范围是
的取值范围是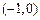 .
.  ……………5分
……………5分 (Ⅱ)当
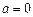 时,
时,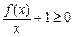 对任意的
对任意的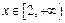 恒成立,
恒成立,即
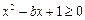 对任意的
对任意的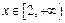 恒成立,
恒成立,也即
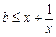 在对任意的
在对任意的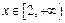 恒成立. ……………7分
恒成立. ……………7分 令
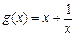 ,则
,则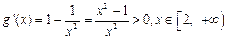 .
.则函数
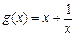 在
在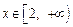 上单调递增,
上单调递增,当
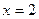 时取最小值
时取最小值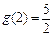 ,故只要
,故只要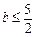 即可.
即可.所以
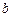 的取值范围是
的取值范围是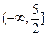 . ……………12分
. ……………12分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
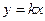 分抛物线
分抛物线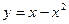 与
与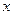 轴所围成图形为面积相等的两个部分,求
轴所围成图形为面积相等的两个部分,求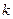 的值.
的值.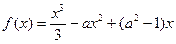 和
和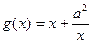
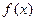 总有两个极值点;
总有两个极值点; 若
若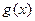 有相同的极值点,求
有相同的极值点,求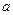 的值.
的值.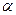 的扇形,制成一个圆锥形容器,扇形的圆心角
的扇形,制成一个圆锥形容器,扇形的圆心角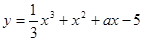 (1)若函数在
(1)若函数在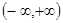 总是单调函数,则
总是单调函数,则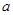 的取值范围是 . (2)若函数在
的取值范围是 . (2)若函数在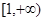 上总是单调函数,则
上总是单调函数,则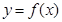 在点
在点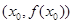 处的 切线方程为
处的 切线方程为 ,则( )
,则( )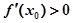
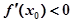
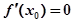
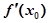 不存在
不存在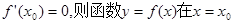 取得极值;
取得极值;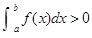 ,则f(x)>0在
,则f(x)>0在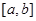 上恒成立;
上恒成立;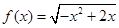 ,则
,则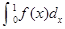 的值为
的值为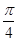 ;
;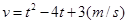 运动,从时刻
运动,从时刻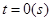 到
到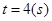 时质点运动的路程为
时质点运动的路程为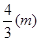 。
。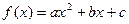 且
且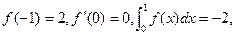 求
求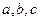 的值
的值 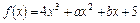 的图象在
的图象在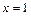 处的切线方程为
处的切线方程为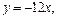
 求函
求函 数
数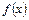 的解析式;
的解析式;