题目内容
4.若不等式(a-3)x2+2(a-3)x-4<0对一切x∈R恒成立,则实数a取值的集合为( )| A. | (-∞,3) | B. | (-1,3) | C. | [-1,3] | D. | (-1,3] |
分析 当a-3=0,不等式即为-4<0,对一切x∈R恒成立,当a≠3时 利用二次函数的性质列出a满足的条件并计算,最后两部分的合并即为所求范围.
解答 解:当a-3=0,即a=3时,不等式即为-4<0,对一切x∈R恒成立 ①
当a≠3时,则须$\left\{\begin{array}{l}{a-3<0}\\{△=4(a-3)^{2}+16(a-3)<0}\end{array}\right.$,
解得 即∴-1<a<3 ②
由①②得实数a的取值范围是(-1,3],
故选:D.
点评 本题考查不等式恒成立的参数取值范围,考查二次函数的性质.注意对二次项系数是否为0进行讨论.

练习册系列答案
相关题目
14.设A是△ABC的最小内角,则sinA+$\sqrt{3}$cosA的取值范围为( )
| A. | ($\sqrt{3}$,2] | B. | [$\sqrt{3}$,2] | C. | ($\sqrt{3}$,2) | D. | ($\frac{\sqrt{3}}{2}$,1] |
19.以下四个数是数列{n(n+2)}的项的是 ( )
| A. | 98 | B. | 99 | C. | 100 | D. | 101 |
16.设ξ~B(18,p),又E(ξ)=9,则p的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
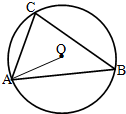 如图所示,在△ABC中,AB=4,AC=2,若O为△ABC的外心.
如图所示,在△ABC中,AB=4,AC=2,若O为△ABC的外心.