题目内容
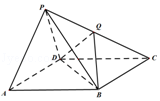
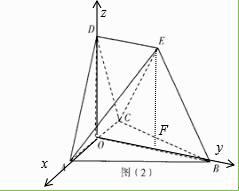
【题目】已知菱形ABCD如图（1）所示，其中∠ACD=60°，AB=2，AC与BD相交于点O，现沿AC进行翻折，使得平面ACD⊥平面ABC，取点E，连接AE，BE，CE，DE，使得线段BE再平面ABC内的投影落在线段OB上，得到的图形如图（2）所示，其中∠OBE=60°，BE=2． 
（Ⅰ）证明：DE⊥AC；
（Ⅱ）求二面角A﹣BE﹣C的余弦值．
【答案】解：（Ⅰ）证明：依题意得△ABC，△ACD都是边长为2的等边三角形，∴DO⊥AC． 又平面ACD⊥平面ABC，平面ACD∩平面ABC=AC，DO面ACD，∴DO⊥面ABC．
作EF⊥面ABC于F，可得F落在BO上，且∠EBF=∠OBE=60°．
在Rt△BEF中，EF=BE 
，
在Rt△DOC中，DO=DC 
，
∵DO⊥面ABC，EF⊥面ABC，所以DO∥EF，又DO=EF，∴四边形DEFO是矩形，
∵OF⊥AC，∴DE⊥AC；
（Ⅱ）以O为原点，OA，OB，OD所在直线分别为x、y、z轴建立空间直角坐标系，
则A（1，0，0），B（0， 
，0），C（﹣1，0，0），E（0， 
）．
故 
）， 
．
设平面BCE的法向量为 
，
由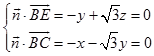 
，可取 
设平面ABE的法向量为 
，
由 
，可取 
cos 
= 
=﹣ 
，
∴二面角A﹣BE﹣C的余弦值为 
【解析】（Ⅰ）依题意得DO⊥AC，又平面ACD⊥平面ABC，得DO⊥面ABC．作EF⊥面ABC于F，可得F落在BO上，可得四边形DEFO是矩形，即证得 DE⊥AC（Ⅱ）以O为原点，OA，OB，OD所在直线分别为x、y、z轴建立空间直角坐标系，则A（1，0，0），B（0， 
，0），C（﹣1，0，0），E（0， 
）．利用向量求解．
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点，需要掌握垂直于同一个平面的两条直线平行才能正确解答此题．
