题目内容
记数列{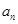 }的前n项和为为
}的前n项和为为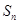 ,且
,且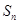 +
+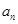 +n=0(n∈N*)恒成立.
+n=0(n∈N*)恒成立.
(1)求证:数列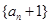 是等比数列;
是等比数列;
(2)已知2是函数f(x)=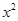 +ax-1的零点,若关于x的不等式f(x)≥
+ax-1的零点,若关于x的不等式f(x)≥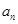 对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
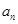 }的前n项和为为
}的前n项和为为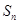 ,且
,且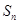 +
+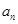 +n=0(n∈N*)恒成立.
+n=0(n∈N*)恒成立.(1)求证:数列
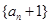 是等比数列;
是等比数列;(2)已知2是函数f(x)=
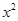 +ax-1的零点,若关于x的不等式f(x)≥
+ax-1的零点,若关于x的不等式f(x)≥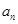 对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.
对任意n∈N﹡在x∈(-∞,λ]上恒成立,求实常数λ的取值范围.(Ⅰ)见解析;(II)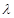 的取值范围
的取值范围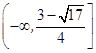 .
.
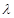 的取值范围
的取值范围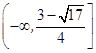 .
.试题分析:(Ⅰ)利用
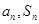 间的关系解答,写出
间的关系解答,写出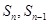 相减,然后根据等比数列定义确定答案;(II)利用(Ⅰ)的结果和等比数列通项公式求出
相减,然后根据等比数列定义确定答案;(II)利用(Ⅰ)的结果和等比数列通项公式求出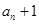 ,然后构造出不等式
,然后构造出不等式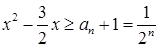 ,求出
,求出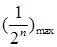 解关于
解关于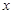 的不等式得出答案.
的不等式得出答案.试题解析:(Ⅰ)
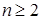 时,
时,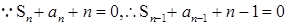 ,两式相减可得,
,两式相减可得,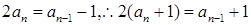 ,
,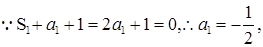
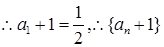 是以
是以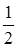 为首项,
为首项,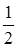 为公比的等比数列. 6分
为公比的等比数列. 6分(II)由(Ⅰ)可得,
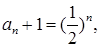
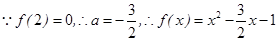 ,
,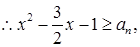 即
即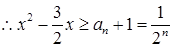 ,
,即
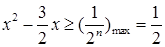 在
在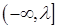 上恒成立,由
上恒成立,由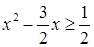 ,即
,即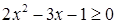 ,
, 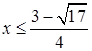 或
或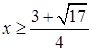 ,
, 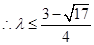 ,
,即所求
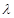 的取值范围
的取值范围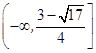 . 12分
. 12分
练习册系列答案
相关题目
 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛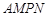 ,要求:B在
,要求:B在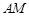 上,D在
上,D在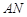 上,对角线
上,对角线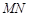 过C点,且矩形
过C点,且矩形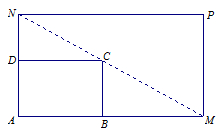
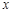 米,矩形
米,矩形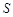 平方米,试用解析式将
平方米,试用解析式将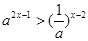
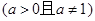 .
.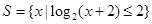 ,集合
,集合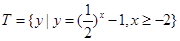 ,求
,求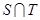 ,
,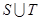 .
.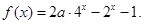
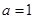 时,求函数
时,求函数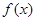 在
在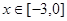 的值域;
的值域;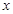 的方程
的方程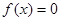 有解,求
有解,求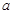 的取值范围.
的取值范围.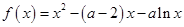 .
.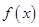 的单调区间
的单调区间 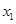 、
、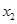 ,且
,且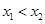 ,求证:
,求证: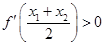 .
.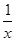 的零点是( )
的零点是( )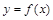 在定义域内给定区间
在定义域内给定区间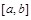 上存在
上存在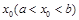 ,满足
,满足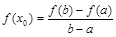 ,则称函数
,则称函数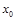 是它的一个均值点,如
是它的一个均值点,如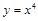 是
是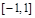 上的平均值函数,0就是它的均值点.现有函数
上的平均值函数,0就是它的均值点.现有函数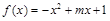 是
是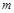 的取值范围是 .
的取值范围是 .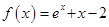 ,
,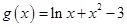 ,若实数
,若实数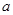 、
、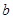 满足
满足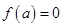 ,
,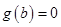 ,则( )
,则( )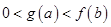
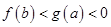
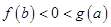

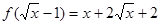 ,则
,则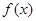 = .
= .