题目内容
设函数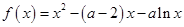 .
.
(1)求函数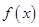 的单调区间
的单调区间
(2)若函数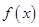 有两个零点
有两个零点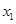 、
、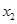 ,且
,且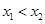 ,求证:
,求证: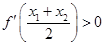 .
.
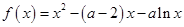 .
.(1)求函数
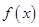 的单调区间
的单调区间 (2)若函数
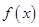 有两个零点
有两个零点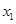 、
、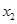 ,且
,且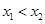 ,求证:
,求证: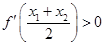 .
.(1)详见解析;(2)详见解析.
试题分析:(1)先求出函数
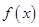 的定义域与导数
的定义域与导数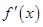 ,并对导数进行因式分解,然后对导数方程的根是否在定义域内进行分类讨论,从而确定函数
,并对导数进行因式分解,然后对导数方程的根是否在定义域内进行分类讨论,从而确定函数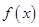 相应的单调区间;(2)先利用函数
相应的单调区间;(2)先利用函数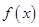 有两个零点
有两个零点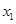 、
、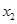 将
将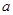 利用
利用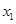 和
和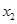 进行表示,于此同时,利用分析法将所要证明的问题进行转化,转化为
进行表示,于此同时,利用分析法将所要证明的问题进行转化,转化为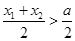 ,并结合前面
,并结合前面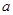 的结果,令
的结果,令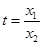 ,构造新函数利用导数来进行证明.
,构造新函数利用导数来进行证明.试题解析:(1)
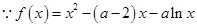 ,定义域为
,定义域为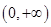 ,
,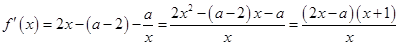 ,由于
,由于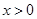 ,
,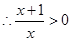 ,
,①当
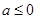 时,对任意
时,对任意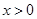 ,
,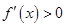 ,则函数
,则函数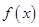 的单调递增区间为
的单调递增区间为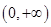 ;
;②当
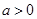 时,令
时,令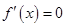 ,解得
,解得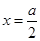 ,
,当
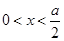 时,
时,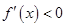 ,当
,当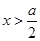 时,
时,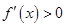 ,
,此时,函数
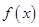 的单调递减区间为
的单调递减区间为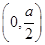 ,单调递增区间为
,单调递增区间为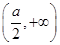 ;
;(2)因为
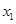 、
、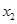 是函数
是函数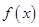 的两个零点,有
的两个零点,有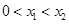 ,
,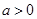
则
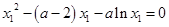 ,
,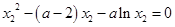 ,
,两式相减得
 ,
,即
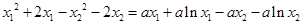
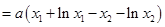
所以
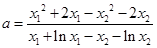
又因为
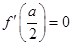 ,当
,当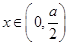 时,
时,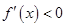 ;当
;当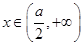 时,
时,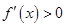
故只要证
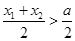 即可,即证明
即可,即证明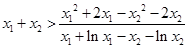 ,
,即证明
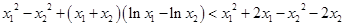 ,
,即证明
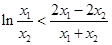 ,
,设
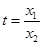
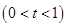 .令
.令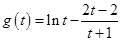 ,
,则
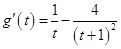
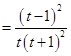 ,因为
,因为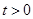 ,所以
,所以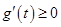 ,当且仅当
,当且仅当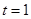 时,
时,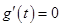
所以
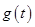 在
在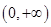 是增函数;又因为
是增函数;又因为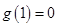 ,所以当
,所以当 时,
时,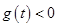 总成立.
总成立.所以原题得证.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
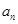 }的前n项和为为
}的前n项和为为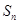 ,且
,且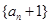 是等比数列;
是等比数列;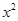 +ax-1的零点,若关于x的不等式f(x)≥
+ax-1的零点,若关于x的不等式f(x)≥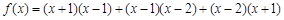 的两个零点分别位于区间
的两个零点分别位于区间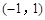 和
和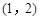 内
内 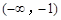 和
和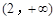 内
内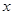 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为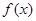 万元,且
万元,且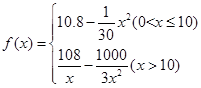
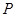 (万元)关于年产品
(万元)关于年产品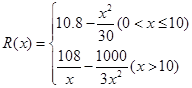
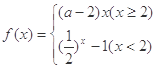 是R上的单调递减函数,则实数a的取值范围为( )
是R上的单调递减函数,则实数a的取值范围为( )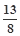 ]
]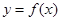 在
在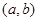 上的导函数为
上的导函数为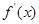 ,
,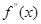 ,若在
,若在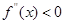 恒成立,则称函数
恒成立,则称函数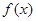 在
在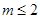 时,
时,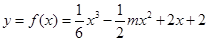 在
在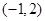 上是“凸函数”,则
上是“凸函数”,则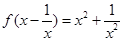 ,则f(3)=___
,则f(3)=___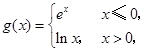 则
则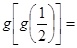 .
.