题目内容
【题目】若以曲线![]() 上任意一点
上任意一点![]() 为切点作切线
为切点作切线![]() ,曲线上总存在异于
,曲线上总存在异于![]() 的点
的点![]() ,以点
,以点![]() 为切点作切线
为切点作切线![]() ,且
,且![]() ,则称曲线
,则称曲线![]() 具有“可平行性”,现有下列命题:
具有“可平行性”,现有下列命题:
①函数![]() 的图象具有“可平行性”;
的图象具有“可平行性”;
②定义在![]() 的奇函数
的奇函数![]() 的图象都具有“可平行性”;
的图象都具有“可平行性”;
③三次函数![]() 具有“可平行性”,且对应的两切点
具有“可平行性”,且对应的两切点![]() ,
, ![]() 的横坐标满足
的横坐标满足![]() ;
;
④要使得分段函数 的图象具有“可平行性”,当且仅当
的图象具有“可平行性”,当且仅当![]() .
.
其中的真命题个数有()
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】由“可平行性”的定义,可得曲线y=f(x)具有“可平行性”,则方程y′=a(a是导数值)至少有两个根。
①函数y=(x2)2+lnx,则y′=2(x2)+ ![]() =
=![]() (x>0),方程
(x>0),方程![]() ,即2x2(4+a)x+1=0,当
,即2x2(4+a)x+1=0,当![]() 时有两个相等正根,不符合题意;
时有两个相等正根,不符合题意;
②定义在(∞,0)∪(0,+∞)的奇函数,如y=x3, 则![]() ,方程
,方程![]() ,当
,当![]() 时有两个相等实数根,不符合题意;
时有两个相等实数根,不符合题意;
③三次函数f(x)=x3x2+ax+b,则f′(x)=3x22x+a,满足题意时, ![]() 的一元二次方程
的一元二次方程![]() 的实数根,即
的实数根,即![]() ,命题③正确;
,命题③正确;
④函数y=ex1(x<0),y′=ex∈(0,1),
函数y=x+1x,y′=11x2=x21x2=11x2,由11x2∈(0,1),得1x2∈(0,1),∴x>1,则m=1.
故要使得分段函数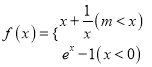 的图象具有“可平行性”,
的图象具有“可平行性”,
当![]() 时,
时, ![]() ,且导函数单调递增,
,且导函数单调递增,
当![]() 时,
时, ![]() 的值域应该是
的值域应该是![]() ,
,
结合幂函数的性质和函数的平移性质可得导函数在![]() 上单调递增,且
上单调递增,且![]() ,
, ![]() ,据此可得m=1.
,据此可得m=1.
真命题个数为2个.
本题选择B选项.

练习册系列答案
相关题目