题目内容
(本小题满分13分)
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。
本小题主要考查解三角形、二次函数等基础知识,绿茶推理论证能力、抽象概括能力、运算求解能力、英语意识,考查函数与方程思想、数形结合思想、化归与转化思想、分类与整合思想。满分13分。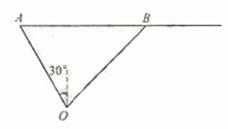
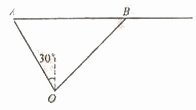
解法一:
(I)设相遇时小艇航行的距离为S海里,则
=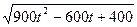
=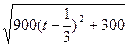
故当 时,
时,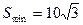 ,此时
,此时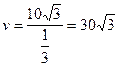
即,小艇以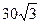 海里/小时的速度航行,相遇时小艇的航行距离最小。
海里/小时的速度航行,相遇时小艇的航行距离最小。
(II)设小艇与轮船在B出相遇,则
故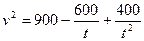
 ,
,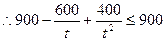
即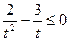 ,解得
,解得
又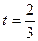 时,
时,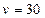
故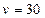 时,t取最小值,且最小值等于
时,t取最小值,且最小值等于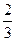
此时,在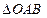 中,有
中,有 ,故可设计寒星方案如下:
,故可设计寒星方案如下:
航行方向为北偏东 ,航行速度为30海里/小时,小艇能以最短时间与轮船相遇
,航行速度为30海里/小时,小艇能以最短时间与轮船相遇
解法二:
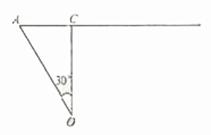
(I)若相遇时小艇的航行距离最小,又轮船沿正东方向匀速行驶,则小艇航行方向为正北方向。
设小艇与轮船在C处相遇。
在 中,
中, ,
,
又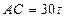 ,
,
此时,轮船航行时间 ,
, 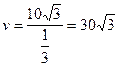
即,小艇以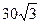 海里/小时的速度航行,相遇时小艇的航行距离最小。
海里/小时的速度航行,相遇时小艇的航行距离最小。
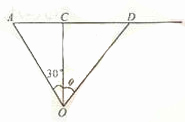
(II)猜想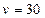 时,小艇能以最短时间与轮船在D出相遇,此时
时,小艇能以最短时间与轮船在D出相遇,此时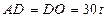
又 ,所以
,所以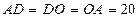 ,解得
,解得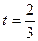
据此可设计航行方案如下:
航行方向为北偏东 ,航行速度为30海里/小时,小艇能以最短时间与轮船相遇
,航行速度为30海里/小时,小艇能以最短时间与轮船相遇
证明如下:
如图,由(I)得 ,
,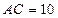 ,
,
故 ,且对于线段
,且对于线段 上任意点P,
上任意点P,
有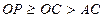 而小艇的最高航行速度只能达到30海里/小时,
而小艇的最高航行速度只能达到30海里/小时,
故小艇与轮船不可能在A,C之间(包含C)的任意位置相遇。
设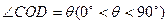 ,则在
,则在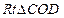 中,
中,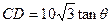 ,
,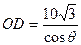
由于从出发到相遇,轮船与小艇所需要的时间分别为 和
和
所以,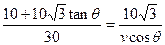
由此可得,
又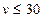 ,故
,故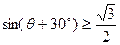
从而,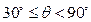
由于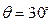 时,
时, 取得最小值,且最小值为
取得最小值,且最小值为
于是,当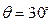 时,
时, 取得最小值,且最小值为
取得最小值,且最小值为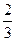
解法三:
(I)同解法一或解法二
(II)设小艇与轮船在B处相遇。依据题意得: ,
,
(
(1) 若 ,则由
,则由
=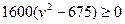
得
解析

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案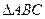 中,已知
中,已知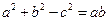 ,且
,且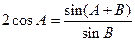 .
.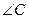 的大小。
的大小。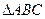 中,
中,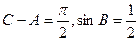
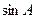
 ,求
,求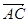 ,
,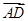 和
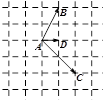
和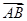 在正方形网格中的位置如图所示,若
在正方形网格中的位置如图所示,若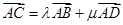 ,则
,则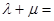 ( )
( )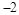
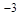
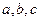 是A,B,C所
是A,B,C所 对的边,S是
对的边,S是 该三角形的面积,且
该三角形的面积,且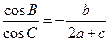

 1)求∠B的大小;
1)求∠B的大小; =4,
=4, ,求
,求
 的值。
的值。 角
角
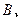
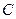 所对的边分别为
所对的边分别为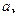
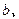
 且
且
 .
.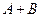 的值;
的值;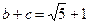 ,求
,求 的值.
的值.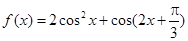
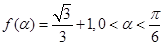 ,求
,求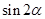 的值;
的值; 中,
中, ,
,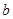 ,
,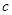 分别是角
分别是角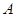 ,
,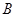 ,
,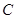 的对边;若
的对边;若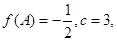
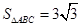 ,求
,求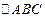 中,
中,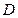 为边
为边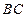 上的一点,
上的一点,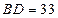 ,
, ,
,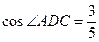 ,求
,求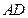 。
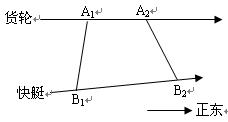
。 海里的速度向正东方航行,快艇按固定方向匀速直线航行,当货轮位于A1处时,快艇位于货轮的东偏南105°方向的B1处,此时两船相距30海里,当货轮航行30分钟到达A2处时,快艇航行到货轮的东偏南45°方向的B2处,此时两船相距
海里的速度向正东方航行,快艇按固定方向匀速直线航行,当货轮位于A1处时,快艇位于货轮的东偏南105°方向的B1处,此时两船相距30海里,当货轮航行30分钟到达A2处时,快艇航行到货轮的东偏南45°方向的B2处,此时两船相距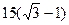 海里。问快艇每小时航行多少海里?
海里。问快艇每小时航行多少海里?