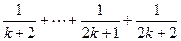题目内容
试证:当n为正整数时,f(n)=32n+2-8n-9能被64整除.
证明略
证明 方法一 (1)当n=1时,f(1)=34-8-9=64,
命题显然成立.
(2)假设当n="k" (k≥1,k∈N*)时,
f(k)=32k+2-8k-9能被64整除.
由于32(k+1)+2-8(k+1)-9=9(32k+2-8k-9)+9·8k+9·9-8(k+1)-9=9(32k+2-8k-9)+64(k+1)
即f(k+1)=9f(k)+64(k+1)
∴n=k+1时命题也成立.
根据(1)(2)可知,对任意的n∈N*,命题都成立.
方法二 (1)当n=1时,f(1)=34-8-9=64,命题显然成立.
(2)假设当n="k" (k≥1,k∈N*)时,f(k)=32k+2-8k-9能被64整除.
由归纳假设,设32k+2-8k-9=64m(m为大于1的自然数),将32k+2=64m+8k+9代入到f(k+1)中得
f(k+1)=9(64m+8k+9)-8(k+1)-9=64(9m+k+1),
∴n=k+1时命题成立.
根据(1)(2)可知,对任意的n∈N*,命题都成立.
命题显然成立.
(2)假设当n="k" (k≥1,k∈N*)时,
f(k)=32k+2-8k-9能被64整除.
由于32(k+1)+2-8(k+1)-9=9(32k+2-8k-9)+9·8k+9·9-8(k+1)-9=9(32k+2-8k-9)+64(k+1)
即f(k+1)=9f(k)+64(k+1)
∴n=k+1时命题也成立.
根据(1)(2)可知,对任意的n∈N*,命题都成立.
方法二 (1)当n=1时,f(1)=34-8-9=64,命题显然成立.
(2)假设当n="k" (k≥1,k∈N*)时,f(k)=32k+2-8k-9能被64整除.
由归纳假设,设32k+2-8k-9=64m(m为大于1的自然数),将32k+2=64m+8k+9代入到f(k+1)中得
f(k+1)=9(64m+8k+9)-8(k+1)-9=64(9m+k+1),
∴n=k+1时命题成立.
根据(1)(2)可知,对任意的n∈N*,命题都成立.

练习册系列答案
相关题目
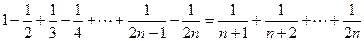
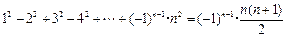 .
. 为常数,且
为常数,且

 有
有 ,求
,求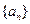 中,
中,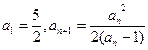
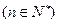 ,用数学归纳法证明:
,用数学归纳法证明: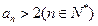
 >
> ,x>y. 求证:
,x>y. 求证: >
> .
.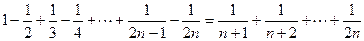 ”时,
”时,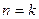 的假设证明
的假设证明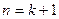 时,如果从等式左边证明右边,则必须证得右边为( )
时,如果从等式左边证明右边,则必须证得右边为( ) 、
、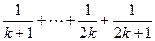 B、
B、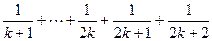

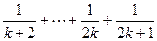 D、
D、