题目内容
设 为常数,且
为常数,且
小题1:证明对任意
小题2:假设对任意 有
有 ,求
,求 的取值范围.
的取值范围.
 为常数,且
为常数,且
小题1:证明对任意

小题2:假设对任意
 有
有 ,求
,求 的取值范围.
的取值范围.小题1:证法一:(ⅰ)当
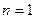 时,由已知
时,由已知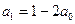 ,等式成立.
,等式成立.(ⅱ)假设当
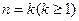 等式成立,即
等式成立,即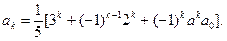
那么
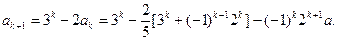
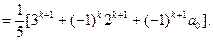
也就是说,当
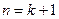 时,等式也成立.
时,等式也成立.根据(ⅰ)和(ⅱ)可知
小题2:由
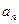 通项公式
通项公式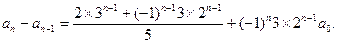
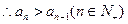 ①
①(ⅰ)当
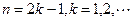 时,①式即为
时,①式即为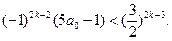
即为
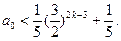 ②
②②式对
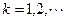 都成立,有
都成立,有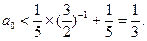
(ⅱ)当
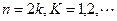 时,
时,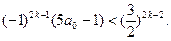
即为
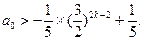 ③
③③式对
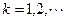 都成立,有
都成立,有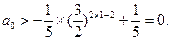
综上,①式对任意
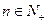 成立,有
成立,有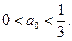
故
 的取值范围为
的取值范围为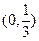
同答案

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
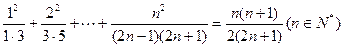 。
。 中,
中, ,求数列
,求数列
 ,则
,则 的最小值是 .
的最小值是 .