题目内容
(选修4—5:不等式选讲)
已知a、b、x、y均为正实数,且 >
> ,x>y. 求证:
,x>y. 求证: >
> .
.
已知a、b、x、y均为正实数,且
 >
> ,x>y. 求证:
,x>y. 求证: >
> .
.略
证法一:(作差比较法)∵ -
-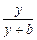 =
=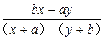 ,又
,又 >
>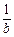 且a、b∈R+,
且a、b∈R+,
∴b>a>0.又x>y>0,∴bx>ay. ∴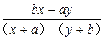 >0,即
>0,即 >
>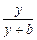 .
.
证法二:(分析法)
∵x、y、a、b∈R+,∴要证 >
>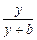 ,只需证明x(y+b)>y(x+a),即证xb>ya.
,只需证明x(y+b)>y(x+a),即证xb>ya.
而由 >
>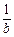 >0,∴b>a>0.又x>y>0,知xb>ya显然成立.故原不等式成立.
>0,∴b>a>0.又x>y>0,知xb>ya显然成立.故原不等式成立.
 -
-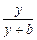 =
=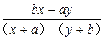 ,又
,又 >
>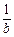 且a、b∈R+,
且a、b∈R+,∴b>a>0.又x>y>0,∴bx>ay. ∴
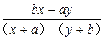 >0,即
>0,即 >
>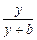 .
.证法二:(分析法)
∵x、y、a、b∈R+,∴要证
 >
>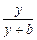 ,只需证明x(y+b)>y(x+a),即证xb>ya.
,只需证明x(y+b)>y(x+a),即证xb>ya.而由
 >
>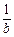 >0,∴b>a>0.又x>y>0,知xb>ya显然成立.故原不等式成立.
>0,∴b>a>0.又x>y>0,知xb>ya显然成立.故原不等式成立.
练习册系列答案
相关题目
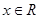 ,
, 恒成立(其中
恒成立(其中 ),求
),求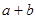 的最大值.
的最大值.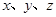 满足
满足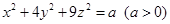 ,且
,且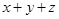 的最大值是7,求
的最大值是7,求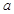 的值.
的值.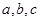 均为正实数,且
均为正实数,且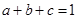 .求
.求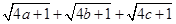 的最大值.
的最大值.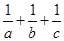 的最小值为( )
的最小值为( ) ,将它沿高AD翻折,使点B 与点C间的距离为
,将它沿高AD翻折,使点B 与点C间的距离为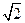 和
和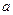 ,且长为
,且长为 )
)