题目内容
1.已知平面向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\overrightarrow{a}•\overrightarrow{b}=2$,($\overrightarrow{c}$$-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的最大值为$\sqrt{3}$+1.分析 根据条件可以得到$\overrightarrow{a},\overrightarrow{b}$夹角为60°,可作$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$,根据条件可以得出OA=2,OB=2,∠AOB=60°,AC⊥BC,从而说明点C在以AB为直径的圆上,从而当OC过圆心时,OC最长,即$|\overrightarrow{c}|$最大,连接AB,△AOB为等边三角形,设圆心为D,从而根据OC=OD+DC便可得出$|\overrightarrow{c}|$的最大值.
解答 解:$|\overrightarrow{a}|=|\overrightarrow{b}|=\overrightarrow{a}•\overrightarrow{b}=2$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{1}{2}$;
∴$<\overrightarrow{a},\overrightarrow{b}>=60°$;
如图,作$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$,则$\overrightarrow{c}-\overrightarrow{a}=\overrightarrow{AC},\overrightarrow{c}-\overrightarrow{b}=\overrightarrow{BC}$;
∵$(\overrightarrow{c}-\overrightarrow{a})•(\overrightarrow{c}-\overrightarrow{b})=0$;
∴$\overrightarrow{AC}•\overrightarrow{BC}=0$;
∴AC⊥BC;
∴点C在以AB为直径的圆上,设圆心为D,D为AB中点;
∠AOB=60°,OA=OB=2;
∴AB=2;
∴圆半径为1;
∴当OC过D点时,OC最大,即$|\overrightarrow{c}|$最大;
此时$OC=OD+DC=2•\frac{\sqrt{3}}{2}+1=\sqrt{3}+1$;
即$|\overrightarrow{c}|$的最大值为$\sqrt{3}+1$.
故答案为:$\sqrt{3}+1$.
点评 考查数量积的计算公式,向量夹角的概念,用有线向量表示向量,以及向量垂直的充要条件,直径所对的圆周角为直角,数形结合解题的方法.

 阅读快车系列答案
阅读快车系列答案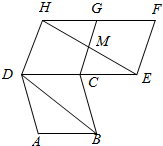 如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )
如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )| A. | |$\overrightarrow{AB}$|=|$\overrightarrow{EF}$| | B. | $\overrightarrow{AB}$与$\overrightarrow{FH}$共线 | C. | $\overrightarrow{BD}$与$\overrightarrow{EH}$共线 | D. | $\overrightarrow{DC}$与$\overrightarrow{EC}$共线 |
| A. | $\frac{1}{3}$<a≤$\frac{1}{2}$ | B. | $\frac{1}{3}$≤a<$\frac{1}{2}$ | ||
| C. | $\frac{1}{3}$<a≤$\frac{1}{2}$或-$\frac{1}{2}$≤a<-$\frac{1}{3}$ | D. | $\frac{1}{3}$≤a<$\frac{1}{2}$或-$\frac{1}{2}$<a≤-$\frac{1}{3}$ |
| A. | sin2+cos2 | B. | cos2-sin2 | C. | sin2-cos2 | D. | ±(cos2-sin2) |