过正方体三个顶点的一个截面截得一个正三棱锥.若正方体棱长为a.求截得正三棱锥的表面积．题目和参考答案——青夏教育精英家教网—

题目内容

18．过正方体三个顶点的一个截面截得一个正三棱锥，若正方体棱长为a，求截得正三棱锥的表面积．

分析由题意可知三棱锥是正四面体，它的表面积就是四个三角形的面积，求出一个三角形的面积即可求解本题．

解答解：由题意可知三棱锥是正四面体，各个三角形的边长为$\sqrt{2}$a，三棱锥的表面积就是四个全等三角形的面积，
即：4×$\frac{\sqrt{3}}{4}•2{a}^{2}$=2$\sqrt{3}$a²．

点评本题考查棱锥的侧面积表面积，考查空间想象能力，计算能力，是基础题．

练习册系列答案

相关题目

8．点的集合M={（x，y）|xy＞0}是指（　　）

	A．	第一象限内点的集合		B．	第三象限内点的集合
	C．	第一、三象限内点的集合		D．	第二、四象限内点的集合

9．

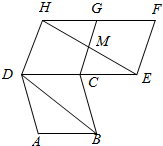如图，四边形ABCD，CEFG，CGFD都是全等的菱形，HE与CG相交于点M，则下列关系不一定成立的是（　　）

A．

|$\overrightarrow{AB}$|=|$\overrightarrow{EF}$|

B．

$\overrightarrow{AB}$与$\overrightarrow{FH}$共线

C．

$\overrightarrow{BD}$与$\overrightarrow{EH}$共线

D．

$\overrightarrow{DC}$与$\overrightarrow{EC}$共线

6．已知关于x的不等式ax²+x＜0的解集中的整数恰有2个，则（　　）

	A．	$\frac{1}{3}$＜a≤$\frac{1}{2}$		B．	$\frac{1}{3}$≤a＜$\frac{1}{2}$
	C．	$\frac{1}{3}$＜a≤$\frac{1}{2}$或-$\frac{1}{2}$≤a＜-$\frac{1}{3}$		D．	$\frac{1}{3}$≤a＜$\frac{1}{2}$或-$\frac{1}{2}$＜a≤-$\frac{1}{3}$

13．化简：$\sqrt{1-2sin（π-2）•cos（π-2）}$得（　　）

3．求函数y=log${\;}_{\frac{1}{2}}$（x²-2x-8）的定义域，值域和单调性．

10．已知向量$\overrightarrow{p}$=（sin（x-$\frac{π}{6}$），cosx），$\overrightarrow{q}$=（cosx，cosx），若函数f（x）=$\overrightarrow{p}$•$\overrightarrow{q}$-$\frac{1}{4}$．
（1）求x$∈[-\frac{5π}{24}，\frac{7π}{24}]$时，函数f（x）的值域；
（2）在△ABC中，a，b，c分别是角A、B、C的对边，若f（A）=$\frac{1}{4}$，且a=2，求BC边上中线的最大值．

3．太阳光线与地面的夹角为30°，一个球在地面的影子是椭圆，那么椭圆的离心率为（　　）

A．

$\frac{{\sqrt{3}}}{2}$

B．

$\frac{{\sqrt{3}}}{3}$

C．

$\frac{{2\sqrt{3}}}{3}$

D．

$\frac{1}{2}$

4．在△ABC中，tan$\frac{A+B}{2}$=2sinC，若AB=1，则△ABC周长的取值范围（2，3]．

试题分类