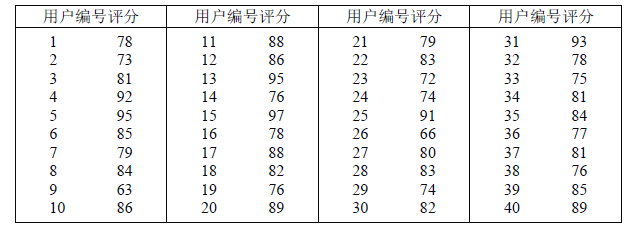
题目内容
【题目】已知各项都是正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求和
,求和![]() ;
;
(3)是否存在正整数![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列?若存在,求出所有满足要求的
成等差数列?若存在,求出所有满足要求的![]() ,
,![]() ,
,![]() ,若不存在,说明理由.
,若不存在,说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在
;(3)存在![]() 或
或![]() ,
,![]() ,
,![]() 满足要求.
满足要求.
【解析】试题分析:
(1)由递推关系可得![]() ,则
,则![]() ,
,![]() 是等差数列,其中公差为1,且
是等差数列,其中公差为1,且![]() ,通项公式为
,通项公式为![]() ,数列
,数列![]() 是等比数列,其中首项为
是等比数列,其中首项为![]() ,公比为
,公比为![]() ,故
,故![]() .
.
(2)结合(1)的结论可得![]() ,则
,则![]() ,
,
(3)假设存在正整数![]() ,使得
,使得![]() 成等差数列,则
成等差数列,则![]() ,
,
而数列![]() 从第二项起单调递减,分类讨论:
从第二项起单调递减,分类讨论:
当![]() 时,
时,![]() ,若
,若![]() ,无解;若
,无解;若![]() ,
,![]() 符合要求,若
符合要求,若![]() ,无解; 故
,无解; 故![]() ,此时
,此时![]() ,可得
,可得![]() ,
,![]() .
.
试题解析:
(1)![]() ①,
①,![]() ②,
②,
②-①得:![]() ,即
,即![]() ,
,
因为![]() 是正数数列,所以
是正数数列,所以![]() ,即
,即![]() ,
,
所以![]() 是等差数列,其中公差为1,
是等差数列,其中公差为1,
在![]() 中,令
中,令![]() ,得
,得![]() ,
,
所以![]() ,
,
由![]() 得
得![]() ,
,
所以数列![]() 是等比数列,其中首项为
是等比数列,其中首项为![]() ,公比为
,公比为![]() ,
,
所以![]() .
.
(2)![]() ,裂项得
,裂项得![]() ,
,
所以,
(3)假设存在正整数![]() ,使得
,使得![]() 成等差数列,则
成等差数列,则![]() ,即
,即![]() ,
,
因为![]() ,所以数列
,所以数列![]() 从第二项起单调递减,
从第二项起单调递减,
当![]() 时,
时,![]() ,
,
若![]() ,则
,则![]() ,此时无解;
,此时无解;
若![]() ,则
,则![]() ,因为
,因为![]() 从第二项起递减,故
从第二项起递减,故![]() ,所以
,所以![]() 符合要求,
符合要求,
若![]() ,则
,则![]() ,即
,即![]() ,不符合要求,此时无解;
,不符合要求,此时无解;
当![]() 时,一定有
时,一定有![]() ,否则若
,否则若![]() ,则
,则![]() ,即
,即![]() ,矛盾,
,矛盾,
所以![]() ,此时
,此时![]() ,令
,令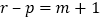 ,则
,则![]() ,所以
,所以![]() ,
,![]() ,
,
综上得:存在![]() 或
或![]() ,
,![]() ,
,![]() 满足要求.
满足要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某组织在某市征集志愿者参加志愿活动,现随机抽出60名男生和40名女生共100人进行调查,统计出100名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比例情况,具体数据如图所示.
(1)根据条件完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为愿意参与志愿活动与性别有关?
的把握认为愿意参与志愿活动与性别有关?

愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)现用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者,再从中抽取2人作为队长,求抽取的2人至少有一名女生的概率.
参考数据及公式:
|
|
|
|
|
|
|
|
|
|
![]() .
.