题目内容
(本小题满分14分)
已知定义在R上的单调函数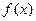 ,存在实数
,存在实数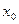 ,使得对于任意实数
,使得对于任意实数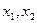 总有
总有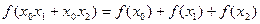 恒成立.(Ⅰ)求
恒成立.(Ⅰ)求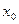 的值;(Ⅱ)若
的值;(Ⅱ)若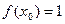 ,且对任意正整数
,且对任意正整数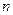 ,有
,有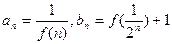 ,记
,记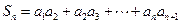 ,
,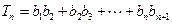 ,比较
,比较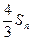 与
与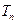 的大小关系;
的大小关系;
(Ⅲ)若不等式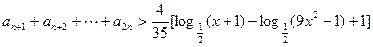 对任意不小于2的正整数
对任意不小于2的正整数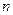 都成立,求
都成立,求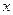 的取值范围.
的取值范围.
已知定义在R上的单调函数
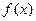 ,存在实数
,存在实数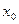 ,使得对于任意实数
,使得对于任意实数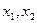 总有
总有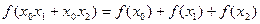 恒成立.(Ⅰ)求
恒成立.(Ⅰ)求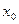 的值;(Ⅱ)若
的值;(Ⅱ)若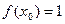 ,且对任意正整数
,且对任意正整数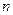 ,有
,有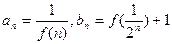 ,记
,记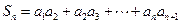 ,
,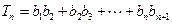 ,比较
,比较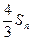 与
与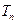 的大小关系;
的大小关系;(Ⅲ)若不等式
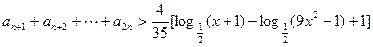 对任意不小于2的正整数
对任意不小于2的正整数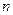 都成立,求
都成立,求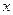 的取值范围.
的取值范围.(Ⅰ)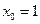 (Ⅱ) 略(Ⅲ)
(Ⅱ) 略(Ⅲ)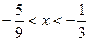 或
或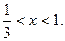
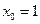 (Ⅱ) 略(Ⅲ)
(Ⅱ) 略(Ⅲ)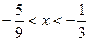 或
或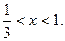
(Ⅰ)令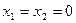 ,得
,得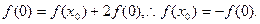 ①
①
令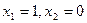 ,得
,得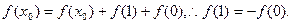 ②
②
由①,②得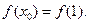
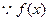 为单调函数,∴
为单调函数,∴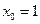 .
.
(Ⅱ)由(Ⅰ)得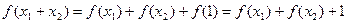 ,
,
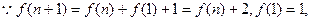
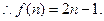
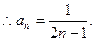
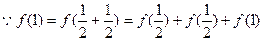
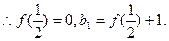
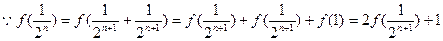 ,
,
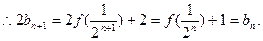
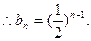
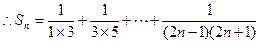
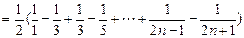
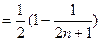
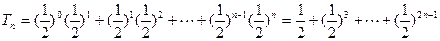

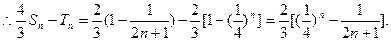
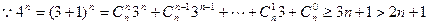 ,
,
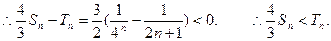
(Ⅲ)令 ,
,
则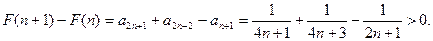
∴当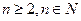 时,
时,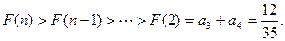
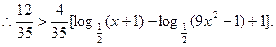 即
即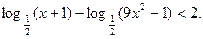
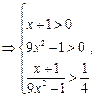 解得
解得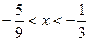 或
或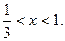
 ,得
,得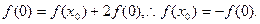 ①
①令
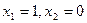 ,得
,得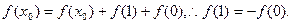 ②
②由①,②得
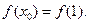
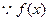 为单调函数,∴
为单调函数,∴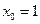 .
.(Ⅱ)由(Ⅰ)得
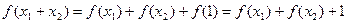 ,
,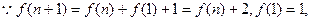
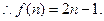
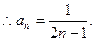
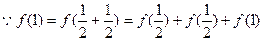
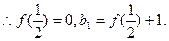
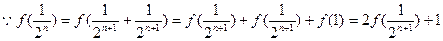 ,
,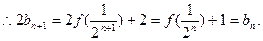
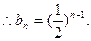
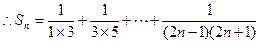
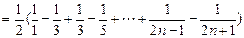
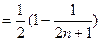
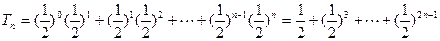

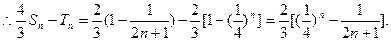
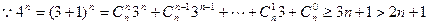 ,
,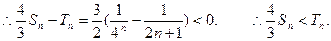
(Ⅲ)令
 ,
,则
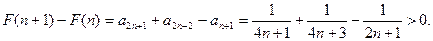
∴当
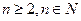 时,
时,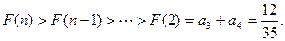
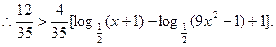 即
即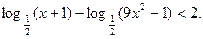
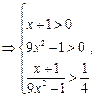 解得
解得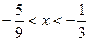 或
或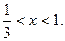

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
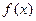 为定义在R上的偶函数,当
为定义在R上的偶函数,当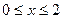 时,
时,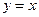 ;当
;当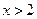 时,
时,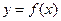 的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分.
的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分.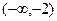 上的解析式;
上的解析式;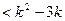 对
对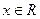 恒成立,求
恒成立,求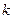 的取值范围。
的取值范围。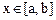 ,总有
,总有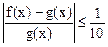 ,则称f(x)可被g(x)替代,试判断函数
,则称f(x)可被g(x)替代,试判断函数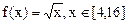 能否被
能否被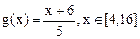 替代,并说明理由.
替代,并说明理由.

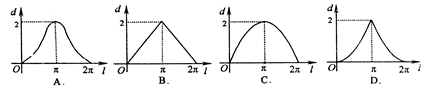
 是单位圆上的一定点,动点
是单位圆上的一定点,动点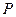 从点
从点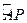 的长为
的长为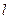 ,弦
,弦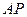 的长为
的长为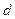 ,则函数
,则函数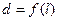 的图像大致是
的图像大致是
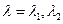 时,连续函数
时,连续函数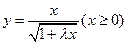 的图像分别对应曲线
的图像分别对应曲线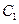 和
和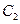 , 则( )
, 则( )

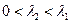
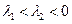
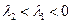
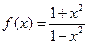 ,则
,则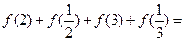 。
。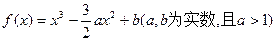 在区间
在区间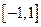 上最大值为1,最小值为
上最大值为1,最小值为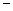 2.(1)求
2.(1)求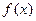 的解析式;(2)若函数
的解析式;(2)若函数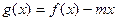 在区间
在区间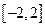 上为减函数,求实数m的取值范围.
上为减函数,求实数m的取值范围.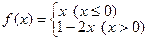 ,则
,则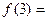 ____
____