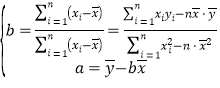题目内容
【题目】已知函数f(x)=ln x+ax2-2x,(a∈R,a≠0)
(1)若函数f(x)的图象在x=1处的切线与x轴平行,求f(x)的单调区间;
(2)若f(x)≤ax在x∈[![]() ,+∞)上恒成立,求a的取值范围.
,+∞)上恒成立,求a的取值范围.
【答案】(1)单调递增区间为(0,+∞),无单调递减区间.(2)-4-4ln 2≤a<0.
【解析】
(1) f '(x)=![]() +2ax-2由f '(1)=1+2a-2=0,解得a=
+2ax-2由f '(1)=1+2a-2=0,解得a=![]() ,得f '(x)=
,得f '(x)=![]() ≥0恒成立,则单调区间可求;(2) f(x)≤ax转化为ln x+ax2-2x-ax≤0,构造函数g(x)=ln x+ax2-2x-ax,x∈[
≥0恒成立,则单调区间可求;(2) f(x)≤ax转化为ln x+ax2-2x-ax≤0,构造函数g(x)=ln x+ax2-2x-ax,x∈[![]() ,+∞),求导求其最大值即可求解
,+∞),求导求其最大值即可求解
(1)函数f(x)=ln x+ax2-2x,定义域为(0,+∞),f '(x)=![]() +2ax-2.
+2ax-2.
由已知f '(1)=1+2a-2=0,解得a=![]() ,
,
于是f '(x)=![]() ≥0恒成立,
≥0恒成立,
从而f(x)的单调递增区间为(0,+∞),无单调递减区间.
(2) f(x)≤ax转化为ln x+ax2-2x-ax≤0,
设g(x)=ln x+ax2-2x-ax,x∈[![]() ,+∞),
,+∞),
则g'(x)=![]() +2ax-2-a=
+2ax-2-a=![]() .
.
①当a<0时,g(x)在[![]() ,+∞)上单调递减,
,+∞)上单调递减,
因而g(![]() )=ln
)=ln![]() +
+![]() a-1-
a-1-![]() a≤0,故-4-4ln 2≤a<0;
a≤0,故-4-4ln 2≤a<0;
②当0<a<2时,![]() ,g(x)在[
,g(x)在[![]() ,
,![]() ]上单调递减,在(
]上单调递减,在(![]() ,+∞)上单调递增,
,+∞)上单调递增,
因而g(x)∈[g(![]() ),+∞),不符合题意;
),+∞),不符合题意;
③当a≥2时,![]() ,g(x)在[
,g(x)在[![]() ,+∞)上单调递增,
,+∞)上单调递增,
因而g(x)∈[g(![]() ),+∞),不符合题意.
),+∞),不符合题意.
综上,-4-4ln 2≤a<0.

【题目】某名校从![]() 年到
年到![]() 年考入清华,北大的人数可以通过以下表格反映出来。(为了方便计算,将
年考入清华,北大的人数可以通过以下表格反映出来。(为了方便计算,将![]() 年编号为
年编号为![]() ,
,![]() 年编为
年编为![]() ,以此类推……)
,以此类推……)
年份 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
(1)将这![]() 年的数据分为人数不少于
年的数据分为人数不少于![]() 人和少于
人和少于![]() 人两组,按分层抽样抽取
人两组,按分层抽样抽取![]() 年,问考入清华、北大的人数不少于20的应抽多少年?在抽取的这
年,问考入清华、北大的人数不少于20的应抽多少年?在抽取的这![]() 年里,若随机的抽取两年恰有一年考入清华、北大的人数不少于
年里,若随机的抽取两年恰有一年考入清华、北大的人数不少于![]() 的概率是多少?;
的概率是多少?;
(2)根据最近![]() 年的数据,利用最小二乘法求出与之间的线性回归方程,并用以预测
年的数据,利用最小二乘法求出与之间的线性回归方程,并用以预测![]() 年该校考入清华、北大的人数。(结果要求四舍五入至个位)
年该校考入清华、北大的人数。(结果要求四舍五入至个位)
参考公式: