题目内容
【题目】在△ABC中,AC=3,BC=4,AB=5,以AB所在直线为轴,三角形面旋转一周形成一旋转体,求此旋转体的表面积和体积.
![]()
【答案】表面积为![]() π,体积为
π,体积为![]() π.
π.
【解析】
由已知三角形ABC为直角三角形,斜边AB为轴旋转一周,所得旋转体是AB边的高CO为底面半径的两个圆锥组成的组合体,计算出底面半径及两个圆锥高的和,代入圆锥体积公式,即可求出旋转体的体积;又由该几何体的表面积是两个圆锥的侧面积之和,分别计算出两个圆锥的母线长,代入圆锥侧面积公式,即可得到答案.
过C点作CD⊥AB,垂足为D.△ABC以AB所在直线为轴旋转一周,所得到的旋转体是两个底面重合的圆锥,如图所示,
这两个圆锥高的和为AB=5,
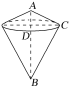
底面半径DC=![]() =
=![]() ,
,
故S表=π·DC·(BC+AC)=![]() π.
π.
V=![]() π·DC2·AD+
π·DC2·AD+![]() π·DC2·BD=
π·DC2·BD=![]() π·DC2(AD+BD)=
π·DC2(AD+BD)=![]() π.
π.
即所得旋转体的表面积为![]() π,体积为
π,体积为![]() π.
π.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目