题目内容
2.已知F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点,且|F1F2|=2,若椭圆C经过点M(0,1).(Ⅰ)求椭圆C的方程;
(Ⅱ)设平行于F1M的直线l(不过椭圆的上下两个顶点)交椭圆C于不同的两点A和B,直线MA和MB的斜率分别为k1,k2,若k1+k2=4,求直线l的方程.
分析 (I)由题意可得2c=2,b=1,又a2=b2+c2,联立解得即可得出.
(II)F1(-1,0),${k}_{M{F}_{1}}$=1.可设直线l的方程为:y=x+m(m≠±1),设A(x1,y1),B(x2,y2).与题意方程联立化为3x2+4mx+2m2-2=0,利用根与系数的关系、向量计算公式可得k1+k2=$\frac{2}{m+1}$=4,解出即可.
解答 解:(I)∵|F1F2|=2,椭圆C经过点M(0,1).
∴2c=2,b=1,又a2=b2+c2,
联立解得a2=2,b=1,
∴椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(II)F1(-1,0),${k}_{M{F}_{1}}$=1.可设直线l的方程为:y=x+m(m≠±1),设A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,化为3x2+4mx+2m2-2=0,
∴x1+x2=$-\frac{4m}{3}$,x1x2=$\frac{2{m}^{2}-2}{3}$.
∴k1+k2=$\frac{{y}_{1}-1}{{x}_{1}}$+$\frac{{y}_{2}-1}{{x}_{2}}$=$\frac{({y}_{1}-1){x}_{2}+({y}_{2}-1){x}_{1}}{{x}_{1}{x}_{2}}$
=$\frac{({x}_{1}+m-1){x}_{2}+({x}_{2}+m-1){x}_{1}}{{x}_{1}{x}_{2}}$
=$\frac{2{x}_{1}{x}_{2}+(m-1)({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}$
=2+$\frac{(m-1)×(-\frac{4m}{3})}{\frac{2{m}^{2}-2}{3}}$
=2+$\frac{-4{m}^{2}+4m}{2{m}^{2}-2}$=$\frac{2}{m+1}$=4,
解得m=-$\frac{1}{2}$.满足△=16m2-4×3×(2m2-2)=22>0,
∴直线l的方程为:2x-2y-1=0.
点评 本题考查了圆锥曲线的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得△>0及其根与系数的关系、斜率计算公式等基础知识与基本技能,考查了推理能力与计算能力,属于难题.

| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
| A. | 42+6$\sqrt{17}$ | B. | 30+6$\sqrt{17}$ | C. | 66 | D. | 44 |
| A. | $\frac{3-2ln2}{4}$ | B. | $\frac{1+2ln2}{4}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{1-ln2}{2}$ |
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).
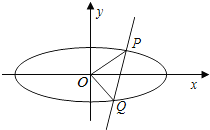
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1). 已知椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,椭圆左、右顶点分别为A、B,且A到椭圆两焦点的距离之和为4.设P为椭圆上不同于A、B的任一点,作PQ⊥x轴,Q为垂足.M为线段PQ中点,直线AM交直线l:x=b于点C,D为线段BC中点(如图).
已知椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1(a>b>0)的离心率e=$\frac{{\sqrt{3}}}{2}$,椭圆左、右顶点分别为A、B,且A到椭圆两焦点的距离之和为4.设P为椭圆上不同于A、B的任一点,作PQ⊥x轴,Q为垂足.M为线段PQ中点,直线AM交直线l:x=b于点C,D为线段BC中点(如图).