题目内容
20.设A={0,1,4},B={1,x2},若B⊆A,则x=( )| A. | 0 | B. | -2 | C. | 0或-2 | D. | 0或±2 |
分析 利用条件B⊆A,得到x2=4或x2=0,求解x之后,利用元素的互异性进行验证求解.
解答 解:∵A={0,1,4},B={1,x2},B⊆A,
则x2=4或x2=0,
解得x=2或x=-2或x=0.
当x=2时,集合B={1,4},满足条件B⊆A.
当x=-2时,B={1,4},满足条件B⊆A.
当x=0时,B={1,0},满足条件B⊆A.
故x=2或x=-2或x=0.
故选:D.
点评 本题主要考查利用集合子集关系确定参数问题,注意求解之后要利用集合元素的互异性进行验证.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
10.在大街上,随机调查339名成人,有关吸烟、不吸烟、患支气管炎、不患支气管炎的数据如右表:根据表中数据,在犯错误的概率不超过0.01 的前提下判断吸烟与患支气管炎是否有关?
附:临界值表
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 患慢性气管炎 | 未患慢性气管炎 | 总计 | |
| 吸烟 | 43 | 162 | 205 |
| 不吸烟 | 13 | 121 | 134 |
| 合计 | 56 | 283 | 339 |
| P(K2>k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
15.△ABC中,角A,B,C所对边的长分别为a,b,c,满足a2+b2=2c2,则cosC的最小值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
5.集合A={x|x2-2x≤0},B={x|y=lg(1-x)},则A∩(∁RB)等于( )
| A. | {x|0<x≤1} | B. | {x|0≤x<1} | C. | {x|1<x≤2} | D. | {x|1≤x≤2} |
12.已知A={x|1<x≤3},B={y|y=($\frac{1}{2}$)x-2,x∈A},则(∁RA)∩B=( )
| A. | (0,1] | B. | (0,1]∪(3,+∞) | C. | (1,3] | D. | $[\frac{1}{2}{,^{\;}}1]$ |
10.从含有甲乙的6名短跑运动员中任选4人参加4*100米接力,问其中甲不能跑第一棒,且乙不能跑第四棒的概率是( )
| A. | $\frac{7}{40}$ | B. | $\frac{7}{30}$ | C. | $\frac{7}{20}$ | D. | $\frac{7}{10}$ |
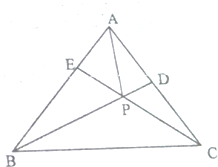 如图,在△ABC中,点D为边AC的中点,3AE=AB,BD=CE交于点P,设$\overrightarrow{a}$=$\overrightarrow{AB}$,$\overrightarrow{b}$=$\overrightarrow{AC}$
如图,在△ABC中,点D为边AC的中点,3AE=AB,BD=CE交于点P,设$\overrightarrow{a}$=$\overrightarrow{AB}$,$\overrightarrow{b}$=$\overrightarrow{AC}$