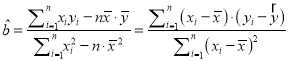题目内容
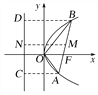
【题目】已知抛物线y2=2px(p>0)的焦点为F,A(x1,y1),B(x2,y2)是过F的直线与抛物线的两个交点,求证:
(1)y1y2=-p2,![]() ;(2)
;(2)![]() 为定值;
为定值;
(3)以AB为直径的圆与抛物线的准线相切.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】试题分析:(1)求出抛物线![]() 的焦点和准线方程,设
的焦点和准线方程,设![]() 直线方程是
直线方程是![]() ,代入拋物线方程,运用韦达定理,结合拋物线方程,即可得证;(2)运用拋物线的定义和韦达定理,计算即可得到定值;(3)求出
,代入拋物线方程,运用韦达定理,结合拋物线方程,即可得证;(2)运用拋物线的定义和韦达定理,计算即可得到定值;(3)求出![]() 的中点坐标,以及
的中点坐标,以及![]() 的长,求得圆的圆心和半径,运用直线和圆相切的条件:
的长,求得圆的圆心和半径,运用直线和圆相切的条件:![]() 即可得证.
即可得证.
试题解析: (1)由已知得抛物线焦点坐标为(![]() ,0).由题意可设直线方程为x=my+
,0).由题意可设直线方程为x=my+![]() ,
,
代入y2=2px,得y2=2p(my+![]() ),即y2-2pmy-p2=0.(*)
),即y2-2pmy-p2=0.(*)
则y1,y2是方程(*)的两个实数根,所以y1y2=-p2.
因为y=2px1,y=2px2,所以yy=4p2x1x2,
所以x1x2=![]() =
=![]() =
=![]() .
.
(2)![]() +
+![]() =
=![]() +
+![]() =
=![]() .
.
因为x1x2=![]() ,x1+x2=|AB|-p,代入上式,
,x1+x2=|AB|-p,代入上式,
得![]() +
+![]() =
=![]() =
=![]() (定值).
(定值).
(3)设AB的中点为M(x0,y0),分别过A,B作准线的垂线,垂足为C,D,过M作准线的垂线,垂足为N,则|MN|=![]() (|AC|+|BD|)=
(|AC|+|BD|)=![]() (|AF|+|BF|)=
(|AF|+|BF|)=![]() |AB|.所以以AB为直径的圆与抛物线的准线相切
|AB|.所以以AB为直径的圆与抛物线的准线相切

【题目】孝感市及周边地区的市民游玩又添新去处啦!孝感熙凤水乡旅游度假区于2017年10月1日正式对外开放.据统计,从2017年10月1日到10月7日参观孝感市熙凤水乡旅游度假区的人数如表所示:
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数(万) | 11 | 13 | 8 | 9 | 7 | 8 | 10 |
(1)把这7天的参观人数看成一个总体,求该总体的众数和平均数(精确到0.1);
(2)用简单随机抽样方法从10月1日到10月4日中抽取2天,它们的参观人数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过1万的概率.
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: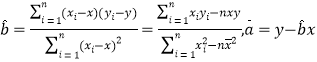 .
.