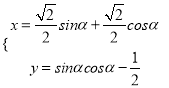题目内容
【题目】已知 ![]() 中,
中, ![]() 分别为两腰上的高、求证:
分别为两腰上的高、求证: ![]()
【答案】【解答】
证明:如图,以 BC 所在直线为 x 轴, BC 的垂直平分线为 y 轴建立平面直角坐标系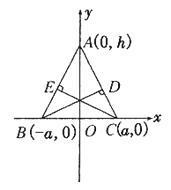
设 ![]()
则直线 AC 的方程为 ,![]()
即: ![]()
直线 AB 的方程为 ,![]()
即: ![]()
由点到直线的距离公式: ,![]()
![]()
∴ ![]() ,即 BD=CE
,即 BD=CE
【解析】本题考查坐标法在几何中的应用、解答本题可通过建立平面直角坐标系,将几何证明问题转化为代数运算问题(1)建立适当的直角坐标系,将平面几何问题转化为解析几何问题,即“形”转化为“数”,再回到“形”中,此为坐标法的基本思想,务必熟练掌握(2)建立坐标系时,要充分利用图形的几何特征、例如,中心对称图形,可利用它的对称中心为坐标原点;轴对称图形,可利用它的对称轴为坐标轴;设中有直角,可考虑以两直角边所在的直线为坐标轴等。

练习册系列答案
相关题目
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下2×2列联表:
喜欢数学课 | 不喜欢数学课 | 合计 | |
男 | 30 | 60 | 90 |
女 | 20 | 90 | 110 |
合计 | 50 | 150 | 200 |
经计算K2≈6.06,根据独立性检验的基本思想,约有(填百分数)的把握认为“性别与喜欢数学课之间有关系”.