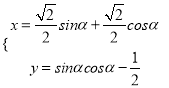题目内容
【题目】已知常数![]() ,在矩形ABCD中,
,在矩形ABCD中, ![]() ,
, ![]() ,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
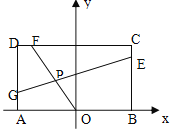
,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且![]() ,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
【答案】见解析
【解析】试题分析:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在的两定点,使得点P到两点距离的和为定值.
试题解析:.按题意有![]()
设![]() 由此有
由此有![]()
直线![]() 的方程为:
的方程为:![]() ①
①
直线![]() 的方程为:
的方程为:![]() ②
②
从①,②消去参数k,得点![]() 的坐标满足方程
的坐标满足方程![]()
整理得  当
当![]() 时,点P的轨迹为圆弧,所以不存在符合题意的两点.
时,点P的轨迹为圆弧,所以不存在符合题意的两点.
当![]() 时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长
时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长
当![]() 时,点P到椭圆两个焦点(
时,点P到椭圆两个焦点(![]() 的距离之和为定值
的距离之和为定值![]()
当![]() 时,点P 到椭圆两个焦点(0,
时,点P 到椭圆两个焦点(0,![]() 的距离之和为定值2
的距离之和为定值2![]() .
.

练习册系列答案
相关题目
【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高二年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名,现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
分数段 |
|
|
|
|
|
|
男 | 3 | 9 | 18 | 15 | 6 | 9 |
女 | 6 | 4 | 5 | 10 | 13 | 2 |
附表及公式:
| 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]()
(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定80分以上者为优分(含80分),请你根据已知条件作出 ![]() 列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.