题目内容
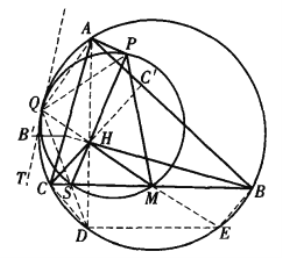
【题目】如图,在![]() 中,AB>AC,H为
中,AB>AC,H为![]() 的垂心,M为边BC的中点,点S在边BC上且满足∠BHM=∠CHS,点A在直线HS上的投影为P.证明:
的垂心,M为边BC的中点,点S在边BC上且满足∠BHM=∠CHS,点A在直线HS上的投影为P.证明:![]() 的外接圆与
的外接圆与![]() 的外接圆相切.
的外接圆相切.

【答案】见解析
【解析】
如图,联结AH并延长,与![]() 的外接圆交于点D
的外接圆交于点D
作![]() ,与
,与![]() 的外接圆交于点E.
的外接圆交于点E.
易知,点D、H关于直线BC对称.
故∠HCB=∠BCD=∠CBE.
则![]() .
.
因此,AE为![]() 外接圆的直径.
外接圆的直径.
又由CH=CD=EB,结合![]() 知四边形CHBE为平行四边形.
知四边形CHBE为平行四边形.
于是,EH过点M.
设B’、C’为点B、C在边AC、AB上的投影.
延长EH,与![]() 的外接圆交于点Q.
的外接圆交于点Q.
由∠AQH=∠AQE=90°=∠APH,得A、Q、B’、H、C’、P六点共圆,且该圆以AH为直径.
由![]()
![]()
由![]()
![]()
结合![]() ,有
,有![]() .
.
则![]() .
.
从而,Q、S、D三点共线.
由![]()
得P、Q、S、M四点共圆,设此圆为圆T.
过点O作![]() 外接圆的切线.
外接圆的切线.
由![]() ,知TQ也为圆T的切线.
,知TQ也为圆T的切线.
故![]() 的外接圆与
的外接圆与![]() 的外接圆相切.
的外接圆相切.

【题目】学生学习的自律性很重要.某学校对自律性与学生成绩是否有关进行了调研,从该校学生中随机抽取了100名学生,通过调查统计得到![]() 列联表的部分数据如下表:
列联表的部分数据如下表:
自律性一般 | 自律性强 | 合计 | |
成绩优秀 | 40 | ||
成绩一般 | 20 | ||
合计 | 50 | 100 |
(1)补全![]() 列联表中的数据;
列联表中的数据;
(2)判断是否有![]() 的把握认为学生的自律性与学生成绩有关.
的把握认为学生的自律性与学生成绩有关.
参考公式及数据: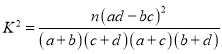 .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】一次数学考试后,对高三文理科学生进行抽样调查,调查其对本次考试的结果满意或不满意,现随机抽取![]() 名学生的数据如下表所示:
名学生的数据如下表所示:
满意 | 不满意 | 总计 | |
文科 | 22 | 18 | 40 |
理科 | 48 | 12 | 60 |
总计 | 70 | 30 | 100 |
(1)根据数据,有多大的把握认为对考试的结果满意与科别有关;
(2)用分层抽样方法在感觉不满意的学生中随机抽取![]() 名,理科生应抽取几人;
名,理科生应抽取几人;
(3)在(2)抽取的![]() 名学生中任取2名,求文科生人数的期望.(
名学生中任取2名,求文科生人数的期望.(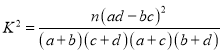 其中
其中![]() )
)
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |