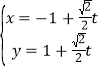题目内容
【题目】已知函数![]() .
.
(1)若![]() 是
是![]() 的极大值点,求
的极大值点,求![]() 的值;
的值;
(2)若![]() 在
在![]() 上只有一个零点,求
上只有一个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)首先对函数![]() 进行求导,然后通过极大值点所对应的导函数值为0即可求出
进行求导,然后通过极大值点所对应的导函数值为0即可求出![]() 的值,最后通过检验即可得出结果;
的值,最后通过检验即可得出结果;
(2)首先可以设方程![]() 并写出方程
并写出方程![]() 的导函数,然后将
的导函数,然后将![]() 在
在![]() 上只有一个零点转化为
上只有一个零点转化为![]() 在
在![]() 上只有一个零点,再利用方程
上只有一个零点,再利用方程![]() 的导函数求出方程
的导函数求出方程![]() 的最小值,最后对方程
的最小值,最后对方程![]() 的最小值与0之间的关系进行分类讨论即可得出结果。
的最小值与0之间的关系进行分类讨论即可得出结果。
(1)![]() ,
,
因为![]() 是
是![]() 的极大值点,所以
的极大值点,所以![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
故![]() 是
是![]() 的极大值点;
的极大值点;
(2)令![]() ,
,![]() ,
,
![]() 在
在![]() 上只有一个零点即
上只有一个零点即![]() 在
在![]() 上只有一个零点,
上只有一个零点,
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增,所以
单调递增,所以![]() .
.
(Ⅰ)当![]() ,即
,即![]() 时,
时,![]() 时,
时,![]() 在
在![]() 上只有一个零点,即
上只有一个零点,即![]() 在
在![]() 上只有一个零点.
上只有一个零点.
(Ⅱ)当![]() ,即
,即![]() 时,取
时,取![]() ,
, ,
,
①若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 和
和![]() 上各有一个零点,即
上各有一个零点,即![]() 在
在![]() 上有2个零点,不符合题意;
上有2个零点,不符合题意;
②当![]() 即
即![]() 时,
时,![]() 只有在
只有在![]() 上有一个零点,即
上有一个零点,即![]() 在
在![]() 上只有一个零点,
上只有一个零点,
综上得,当![]() 时,
时,![]() 在
在![]() 上只有一个零点。
上只有一个零点。

【题目】为了解人们对“2019年3月在北京召开的第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议”的关注度,某部门从年龄在15岁到65岁的人群中随机调查了100人,并得到如图所示的年龄频率分布直方图,在这100人中关注度非常髙的人数与年龄的统计结果如右表所示:

年龄 | 关注度非常高的人数 |
| 15 |
| 5 |
| 15 |
| 23 |
| 17 |
(Ⅰ)由频率分布直方图,估计这100人年龄的中位数和平均数;
(Ⅱ)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过
列联表,据此表,能否在犯错误的概率不超过![]() 的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?
的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?
(Ⅲ)按照分层抽样的方法从年龄在35岁以下的人中任选六人,再从六人中随机选两人,求两人中恰有一人年龄在25岁以下的概率是多少.
45岁以下 | 45岁以上 | 总计 | |
非常髙 | |||
一般 | |||
总计 |
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.他们的调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为,了解阿基米德与选择文理科有关?
的把握认为,了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | |||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取3人,用![]() 表示这3人中文科生的人数,求
表示这3人中文科生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,
,![]() .
.
【题目】为了解中学生对交通安全知识的掌握情况,从农村中学和城镇中学各选取100名同学进行交通安全知识竞赛.下图1和图2分别是对农村中学和城镇中学参加竞赛的学生成绩按![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
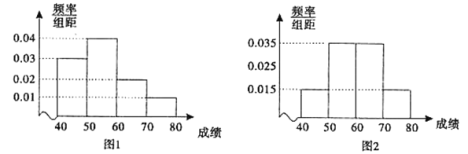
(Ⅰ)分别估算参加这次知识竞赛的农村中学和城镇中学的平均成绩;
(Ⅱ)完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
农村中学 | |||
城镇中学 | |||
合计 |
附:![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |