题目内容
(本小题满分12分)已知椭圆 :
: (
( )的离心率为
)的离心率为 ,过右焦点
,过右焦点 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆 于
于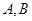 两点,
两点, 为弦
为弦 的中点。
的中点。
(1)求直线 (
( 为坐标原点)的斜率
为坐标原点)的斜率 ;
;
(2)设 椭圆
椭圆 上任意一点,且
上任意一点,且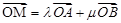 ,求
,求 的最大值和最小值.
的最大值和最小值.
 :
: (
( )的离心率为
)的离心率为 ,过右焦点
,过右焦点 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆 于
于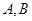 两点,
两点, 为弦
为弦 的中点。
的中点。(1)求直线
 (
( 为坐标原点)的斜率
为坐标原点)的斜率 ;
;(2)设
 椭圆
椭圆 上任意一点,且
上任意一点,且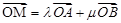 ,求
,求 的最大值和最小值.
的最大值和最小值.(1)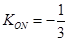 , (2)
, (2)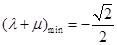
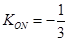 , (2)
, (2)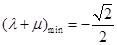
试题分析:(1)设椭圆的焦距为2c,因为
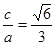 ,所以有
,所以有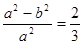 ,故有
,故有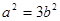 。从而椭圆C的方程可化为:
。从而椭圆C的方程可化为: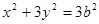 ① …………2分
① …………2分 易知右焦点F的坐标为(
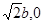 ),
),据题意有AB所在的直线方程为:
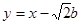 ② …………4分
② …………4分 由①,②有:
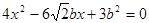 ③
③设
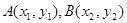 ,弦AB的中点
,弦AB的中点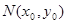 ,由③及韦达定理有:
,由③及韦达定理有: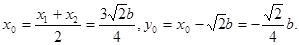
所以
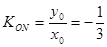 ,即为所求。 …………6分
,即为所求。 …………6分 (2)设
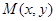 ,由1)中各点的坐标有:
,由1)中各点的坐标有: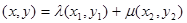 ,所以
,所以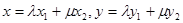 。
。 又点在椭圆C上,所以有
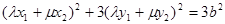 整理为
整理为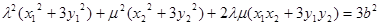 。 ④………8分
。 ④………8分由③有:
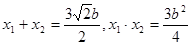 。
。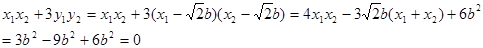 ⑤
⑤又A﹑B在椭圆上,故有
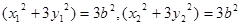 ⑥
⑥将⑤,⑥代入④可得:
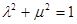 。 …………10分
。 …………10分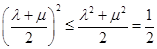 ,故有
,故有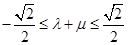
所以
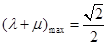 ,
,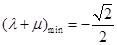 …………12分
…………12分点评:圆锥曲线的问题一般来说计算量大,对运算能力要求很高,寻求简洁、合理的运算途径很重要,在解答时注意以下的转化:⑴若直线与圆锥曲线有两个交点,对待交点坐标是“设而不求”的原则,要注意应用韦达定理处理这类问题 ; ⑵与弦的重点有关问题求解常用方法一韦达定理法 二 点差法;⑶平面向量与解析几何综合题,遵循的是平面向量坐标化,应用的是平面向量坐标运算法则还有两向量平行、垂直来解决问题,这就要求同学们在基本概念、基本方法、基本能力上下功夫.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
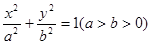 ,左焦点
,左焦点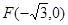 ,且离心率
,且离心率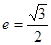
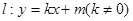 与椭圆C交于不同的两点
与椭圆C交于不同的两点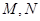 (
(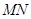 为直径的圆经过椭圆C的右顶点A. 求证:直线
为直径的圆经过椭圆C的右顶点A. 求证:直线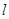 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.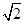 ,离心率e=
,离心率e=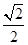 ,过右焦点F的直线l交椭圆于P、Q两点.
,过右焦点F的直线l交椭圆于P、Q两点.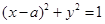 与双曲线
与双曲线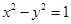 的渐近线相切,则
的渐近线相切,则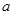 的值是 _______.
的值是 _______. 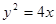 的焦点为F,过抛物线在第一象限部分上一点P的切线为
的焦点为F,过抛物线在第一象限部分上一点P的切线为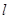 ,过P点作平行于
,过P点作平行于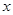 轴的直线
轴的直线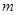 ,过焦点F作平行于
,过焦点F作平行于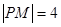 ,则点P的坐标为 。
,则点P的坐标为 。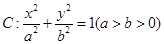 ,F1,F2为其左、右焦点,P为椭圆C上任一点,
,F1,F2为其左、右焦点,P为椭圆C上任一点,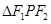 的重心为G,内心I,且有
的重心为G,内心I,且有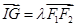 (其中
(其中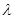 为实数),椭圆C的离心率e=( )
为实数),椭圆C的离心率e=( )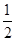
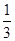
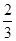
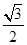
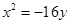 的焦点相同,则双曲线C的标准方程是( )
的焦点相同,则双曲线C的标准方程是( )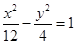
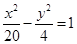
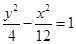
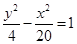
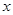 轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线
轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线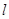 在
在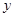 轴上的截距为
轴上的截距为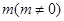 ,
,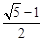 的椭圆称为“优美椭圆”.设
的椭圆称为“优美椭圆”.设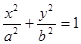
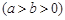 为“优美椭圆”,F、A分别是左焦点和右顶点,B是短轴的一个端点,则
为“优美椭圆”,F、A分别是左焦点和右顶点,B是短轴的一个端点,则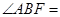 ( )
( )