题目内容
 如图,在正方体ABCD-A1B1C1D1中,点E、F分别是AB、C1D1的中点.
如图,在正方体ABCD-A1B1C1D1中,点E、F分别是AB、C1D1的中点.
(1)证明:点A1、F、C、E在同一平面内;
(2)若点G、H分别是DD1、B1C1的中点,证明:GH⊥平面A1FCE.
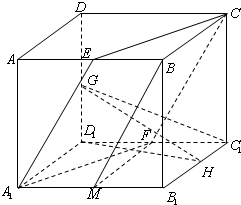 证明:(1)作A1B1的中点M,并连接BM、FM
证明:(1)作A1B1的中点M,并连接BM、FM依题意得EB与A1M平行且相等…(1分)
∴四边形A1MBE是平行四边形∴A1E∥MB…(2分)
又依题意得BC与MF平行且相等∴四边形MFCB是平行四边形…(3分)
∴MB∥FC…(4分)
∴A1E∥FC…(5分)
∴点A1、F、C、E在同一平面内…(6分)
(2)由GD1⊥平面A1B1C1D1,且A1F?平面A1B1C1D1∴GD1⊥A1F…(7分)
又由F、H分别是C1D1、B1C1的中点,∴Rt△A1FD1≌Rt△D1HC1
∴∠D1A1F=∠HD1C1
又∵∠D1A1F+∠D1FA1=90°∴∠HD1C1+∠D1FA1=90°∴D1H⊥A1F…(9分)
而D1H∩D1G=D1,D1H,D1G?平面D1HG
∴A1F⊥平面D1HG,而GH?平面D1HG
∴A1F⊥GH…(11分)
同理可证CF⊥GH…(13分)
而CF∩A1F=F,CF,A1F?平面A1FCE.
∴GH⊥平面A1FCE.…(14分)
分析:(1)作A1B1的中点M,并连接BM、FM,证明四边形A1MBE是平行四边形,四边形MFCB是平行四边形,即可证明点A1、F、C、E在同一平面内.
(2)通过证明A1F⊥平面D1HG,说明A1F⊥GH,CF⊥GH,然后利用直线与平面垂直的判定定理证明GH⊥平面A1FCE.
点评:本题考查四点共面,直线与平面垂直的判定定理的应用,考查空间想象能力与计算能力.

练习册系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )