题目内容
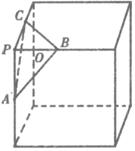
如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记M=| 1 |
| PO2 |
| 1 |
| PA2 |
| 1 |
| PB2 |
| 1 |
| PC2 |
分析：根据平面中直角三角形的勾股定理类比得，S△ABC2=S△PAB2+S△PBC2+S△PAC2，利用等体积法进行比较，即可求出所求．
解答：解：根据平面中直角三角形的勾股定理类比得，S△ABC2=S△PAB2+S△PBC2+S△PAC2①，
由等体积法得 S△ABC•PO=
PA•PB•PC，
∴
•PO2=
PA2•PB2•PC2②，
①÷②整理得M=N．
故答案为：M=N．
由等体积法得 S△ABC•PO=
| 1 |
| 2 |
∴
| S | 2 △ABC |
| 1 |
| 4 |
①÷②整理得M=N．
故答案为：M=N．
点评：本题考查了直角三角形的性质及等面积法和等体积法的应用，同时考查了转化与划归的思想和类比的思想，是一道基础题．
练习册系列答案
相关题目
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
，如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记M=
，那么M、N的大小关系是_____________.
则 （ ）