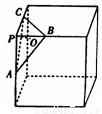
题目内容
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则| 1 |
| h2 |
| 1 |
| a2 |
| 1 |
| b2 |
分析:本题考查的知识点是类比推理,由平面图形的性质类比猜想空间几何体的性质,一般的思路是:点到线,线到面,或是二维变三维;由题目中Rt△ABC中两直角边为a、b,斜边c上的高为h,则
=
+
中的结论是二维边与边的关系,类比后的结论应该为三维的边与边的关系.
| 1 |
| h2 |
| 1 |
| a2 |
| 1 |
| b2 |
解答:解:由平面图形的性质类比猜想空间几何体的性质,
一般的思路是:点到线,线到面,或是二维到三维
由题目中Rt△ABC中两直角边为a、b,斜边c上的高为h,
则
=
+
中的结论是二维的边与边的关系,
类比后的结论应该为三维的边与边的关系,
故可猜想:
=
+
+
,
故答案为:
=
+
+
.
一般的思路是:点到线,线到面,或是二维到三维
由题目中Rt△ABC中两直角边为a、b,斜边c上的高为h,
则
| 1 |
| h2 |
| 1 |
| a2 |
| 1 |
| b2 |
类比后的结论应该为三维的边与边的关系,
故可猜想:
| 1 |
| PO2 |
| 1 |
| PA2 |
| 1 |
| PB2 |
| 1 |
| PC2 |
故答案为:
| 1 |
| PO2 |
| 1 |
| PA2 |
| 1 |
| PB2 |
| 1 |
| PC2 |
点评:由平面图形的性质类比猜想空间几何体的性质,一般的思路是:点到线,线到面,或是二维变三维;由题目中Rt△ABC中两直角边为a、b,斜边c上的高为h,则
=
+
中的结论是二维边与边的关系,类比后的结论应该为三维的边与边的关系.
| 1 |
| h2 |
| 1 |
| a2 |
| 1 |
| b2 |

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则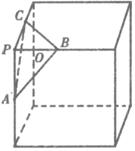
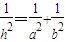 ,如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记M=
,如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记M=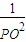 ,N=
,N=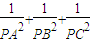 ,那么M、N的大小关系是 .
,那么M、N的大小关系是 .