题目内容
【题目】设正项数列
的前
项和
，且满足
.
（Ⅰ）计算
的值，猜想的通项公式，并证明你的结论；
（Ⅱ）设
是数列
的前项和，证明：
.
【答案】(1) 
（2）见解析
【解析】试题分析：（1）先根据
关系，将条件转化为项与项递推关系，依次代入求解，可得
的值，根据规律猜想，利用项与项递推关系及归纳假设证明n=k+1时情况（2）利用放缩裂项求和：
，也可直接利用数学不等式进行证明
试题解析：（Ⅰ）解：当n=1时，
，得
；
，得
；
，得
.
猜想
证明：（ⅰ）当n=1时，显然成立.
（ⅱ）假设当n=k时，
则当n=k+1时，
结合
，解得
于是对于一切的自然数
，都有
（Ⅱ）证法一：因为，
证法二：数学归纳法
证明：（ⅰ）当n=1时，
，
，
（ⅱ）假设当n=k时，
则当n=k+1时，
要证：
只需证：
由于
所以
于是对于一切的自然数，都有
练习册系列答案
阅读快车系列答案
相关题目
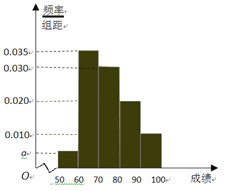
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均分；
（3）现用分层抽样的方法从第3、4、5组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率？
