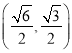题目内容
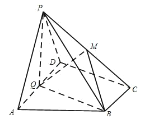
【题目】(本小题满分12分)在如图所示的五面体中,面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是边长为2的正三角形.
是边长为2的正三角形.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.

【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据条件证明出
,根据条件证明出![]() 和
和![]() 即可;
即可;
(2)分别以直线![]() 为
为![]() 轴和
轴和![]() 轴,
轴, ![]() 点为坐标原点,建立空间直角坐标系,求出平面
点为坐标原点,建立空间直角坐标系,求出平面![]() 和平面
和平面![]() 的法向量,即可求得二面角
的法向量,即可求得二面角![]() 的余弦值.
的余弦值.
试题解析:
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,依题意易知
,依题意易知![]() ,
,
平面![]() 平面
平面![]() 平面
平面![]()
![]() .
.
又![]()
![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .
.
在![]() 和
和![]() 中,
中, ![]()
![]() .
.
因为![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
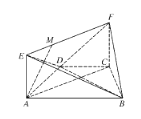
(2)分别以直线![]() 为
为![]() 轴和
轴和![]() 轴,
轴, ![]() 点为坐标原点,建立空间直角坐标系,如图所示,
点为坐标原点,建立空间直角坐标系,如图所示,
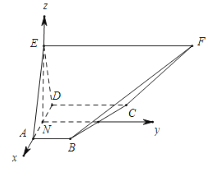
依题意有: ![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,由
,由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,令
,令![]() ,可得
,可得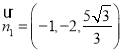 .
.
又平面![]() 的一个法向量
的一个法向量![]() ,所以
,所以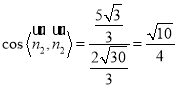 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
注:用其他方法同样酌情给分.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
【题目】现从某班的一次期末考试中,随机的抽取了七位同学的数学(满分150分)、物理(满分110分)成绩如下表所示,数学、物理成绩分别用特征量![]() 表示,
表示,
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
求![]() 关于t的回归方程;
关于t的回归方程;
(2)利用(1)中的回归方程,分析数学成绩的变化对物理成绩的影响,并估计该班某学生数学成绩130分时,他的物理成绩(精确到个位).
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
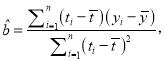
![]() .
. ![]()