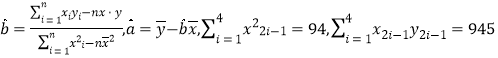题目内容
【题目】(不等式选讲)
已知函数![]() .
.
(1)若![]() ,解不等式
,解不等式![]() ;
;
(2)若不等式![]() 在R上恒成立,求实数
在R上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)[2,+∞).(2){a|a≥2或a≤-4}.
【解析】试题分析:(1)分x<-1,-1≤x≤3,x>3三种情况去掉绝对值讨论即可.
(2)由绝对值三角不等式的性质可得|x+a|+|x-1|≥|a+1|,只需|a+1|≥3,求解即可.
试题解析:(1)依题意,|x+1|+|x-3|≤2x.
当x<-1时,原不等式化为-1-x+3-x≤2x,解得x≥![]() ,故无解;
,故无解;
当-1≤x≤3时,原不等式化为x+1+3-x≤2x,解得x≥2,故2≤x≤3;
当x>3时,原不等式化为x+1+x-3≤2x,即-2≤0恒成立.
综上所述,不等式f(x)+|x-3|≤2x的解集为[2,+∞).
(2)f(x)+|x-1|≥3|x+a|+|x-1|≥3恒成立,
由|x+a|+|x-1|≥|a+1|可知,只需|a+1|≥3即可,
故a≥2或a≤-4,即实数a的取值范围为{a|a≥2或a≤-4}.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目